Cách Tìm Tiệm Cận Xiên Chuẩn Xác: Hướng Dẫn Chi Tiết Từ A-Z

Khi học về hàm số và đồ thị, khái niệm tiệm cận luôn đóng vai trò quan trọng trong việc phác thảo hình dạng của đồ thị tại các điểm vô cùng. Trong số các loại tiệm cận, cách tìm tiệm cận xiên thường gây nhiều bối rối cho học sinh và sinh viên. Bài viết này sẽ cung cấp một hướng dẫn toàn diện, từng bước một để giúp bạn nắm vững phương pháp xác định tiệm cận xiên của một hàm số.

Tiệm Cận Xiên Là Gì? Định Nghĩa Và Ý Nghĩa Trong Đồ Thị Hàm Số

Tiệm cận xiên (tiếng Anh: Oblique Asymptote) là một đường thẳng có dạng y = ax + b (với a ≠ 0) mà đồ thị của hàm số y = f(x) "tiến gần" đến khi x dần tới +∞ hoặc -∞. Nói cách khác, khoảng cách giữa điểm trên đồ thị và đường thẳng này sẽ tiến về 0 khi x tiến ra vô cùng.

Ý nghĩa của tiệm cận xiên là nó cho chúng ta biết xu hướng hành vi của hàm số khi biến số độc lập trở nên rất lớn hoặc rất nhỏ. Việc xác định tiệm cận xiên là một công cụ hữu ích để phác thảo đồ thị, đặc biệt đối với các hàm phân thức hoặc các hàm phức tạp khác mà không cần phải vẽ chính xác từng điểm.

"Tiệm cận không chỉ là một khái niệm toán học khô khan, nó là 'kim chỉ nam' giúp chúng ta hình dung ra 'bức tranh lớn' của hàm số khi nó vươn tới vô cực. Nắm vững cách tìm tiệm cận xiên sẽ mở ra cánh cửa hiểu biết sâu sắc hơn về hành vi giới hạn của các hàm số."

Khi Nào Hàm Số Có Tiệm Cận Xiên? Điều Kiện Cần Và Đủ

Không phải hàm số nào cũng có tiệm cận xiên. Có những điều kiện cụ thể để một hàm số có thể sở hữu tiệm cận xiên. Đối với hàm số dạng phân thức hữu tỉ y = P(x) / Q(x), tiệm cận xiên tồn tại khi và chỉ khi bậc của đa thức P(x) (tử số) lớn hơn bậc của đa thức Q(x) (mẫu số) đúng một đơn vị.

Đối với các hàm số tổng quát hơn, điều kiện tồn tại tiệm cận xiên y = ax + b là:

• Tồn tại giới hạn hữu hạn của a = lim (x→±∞) [f(x) / x] và a ≠ 0.
• Tồn tại giới hạn hữu hạn của b = lim (x→±∞) [f(x) - ax].

Nếu một trong hai giới hạn trên không tồn tại hoặc không hữu hạn, thì hàm số không có tiệm cận xiên.

Cách Tìm Tiệm Cận Xiên Chi Tiết: Phương Pháp Giải Từng Bước

Để tìm tiệm cận xiên của một hàm số y = f(x), chúng ta sẽ đi theo hai bước cơ bản để xác định các hệ số a và b của phương trình đường thẳng y = ax + b.

1. Bước 1: Xác Định Hệ Số Góc 'a'

Hệ số góc a của tiệm cận xiên được tính bằng công thức giới hạn sau:

        a = lim (x→+∞) [f(x) / x]
        Hoặc
        a = lim (x→-∞) [f(x) / x]
    

Bạn cần tính giới hạn này khi x tiến về +∞ và -∞ một cách riêng biệt, vì có thể có hai tiệm cận xiên khác nhau (một cho x→+∞ và một cho x→-∞), mặc dù trong nhiều trường hợp chúng trùng nhau.

Lưu ý: Nếu a = 0, thì tiệm cận đó là tiệm cận ngang (không phải tiệm cận xiên). Nếu a không tồn tại hoặc bằng ±∞, thì không có tiệm cận xiên.

2. Bước 2: Xác Định Tung Độ Gốc 'b'

Sau khi đã tìm được giá trị a, ta sẽ tiếp tục tìm hệ số b bằng công thức giới hạn sau:

        b = lim (x→+∞) [f(x) - ax]
        Hoặc
        b = lim (x→-∞) [f(x) - ax]
    

Tương tự như khi tìm a, bạn cũng cần tính giới hạn này cho cả x→+∞ và x→-∞. Nếu b không tồn tại hoặc bằng ±∞, thì không có tiệm cận xiên.

3. Ví Dụ Minh Họa Cách Tìm Tiệm Cận Xiên

Hãy cùng xét ví dụ sau để hiểu rõ hơn cách tìm tiệm cận xiên:

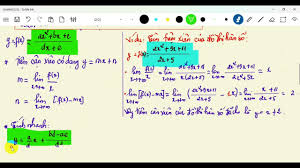
Ví dụ: Tìm tiệm cận xiên của hàm số y = (2x² - 3x + 1) / (x - 2).

1. Kiểm tra điều kiện:

   Đây là hàm phân thức hữu tỉ. Bậc của tử số là 2, bậc của mẫu số là 1. Bậc tử lớn hơn bậc mẫu đúng một đơn vị (2 - 1 = 1), nên hàm số có khả năng có tiệm cận xiên.

2. Tính 'a':

                   a = lim (x→±∞) [f(x) / x]
                   a = lim (x→±∞) [(2x2 - 3x + 1) / (x - 2) / x]
                   a = lim (x→±∞) [(2x2 - 3x + 1) / (x2 - 2x)]
               

   Để tính giới hạn này, ta chia cả tử và mẫu cho x² (bậc cao nhất của mẫu số mới):

                   a = lim (x→±∞) [(2 - 3/x + 1/x2) / (1 - 2/x)]
                   a = (2 - 0 + 0) / (1 - 0) = 2
               

   Vậy, a = 2.

3. Tính 'b':

                   b = lim (x→±∞) [f(x) - ax]
                   b = lim (x→±∞) [(2x2 - 3x + 1) / (x - 2) - 2x]
               

   Để tính giới hạn này, ta quy đồng mẫu số:

                   b = lim (x→±∞) [(2x2 - 3x + 1 - 2x(x - 2)) / (x - 2)]
                   b = lim (x→±∞) [(2x2 - 3x + 1 - 2x2 + 4x) / (x - 2)]
                   b = lim (x→±∞) [(x + 1) / (x - 2)]
               

   Chia cả tử và mẫu cho x (bậc cao nhất của mẫu số):

                   b = lim (x→±∞) [(1 + 1/x) / (1 - 2/x)]
                   b = (1 + 0) / (1 - 0) = 1
               

   Vậy, b = 1.

4. Kết luận:

   Tiệm cận xiên của hàm số là đường thẳng có phương trình y = 2x + 1.

Một phương pháp khác để tìm tiệm cận xiên cho hàm phân thức là chia đa thức tử cho đa thức mẫu. Phần thương (không tính phần dư) chính là phương trình của tiệm cận xiên. Ví dụ trên, khi chia (2x² - 3x + 1) cho (x - 2), ta được 2x + 1 (dư 3). Do đó, tiệm cận xiên là y = 2x + 1.

Phân Biệt Tiệm Cận Xiên, Tiệm Cận Ngang Và Tiệm Cận Đứng

Để hiểu rõ hơn về cách tìm tiệm cận xiên, việc phân biệt nó với các loại tiệm cận khác là rất quan trọng:

Loại Tiệm Cận	Dạng Phương Trình	Điều Kiện Tồn Tại	Ý Nghĩa Đồ Thị
Tiệm Cận Xiên	y = ax + b (a ≠ 0)	lim (x→±∞) [f(x)/x] = a ≠ 0 và lim (x→±∞) [f(x) - ax] = b (hữu hạn). Đối với phân thức, bậc tử hơn bậc mẫu 1.	Đồ thị tiến gần đường thẳng xiên khi x ra vô cùng.
Tiệm Cận Ngang	y = b	lim (x→±∞) f(x) = b (hữu hạn). Đối với phân thức, bậc tử nhỏ hơn hoặc bằng bậc mẫu.	Đồ thị tiến gần đường thẳng ngang khi x ra vô cùng. Là trường hợp đặc biệt của tiệm cận xiên khi a = 0.
Tiệm Cận Đứng	x = x₀	lim (x→x₀±) f(x) = ±∞. Thường xảy ra tại các điểm làm mẫu số bằng 0 (đối với phân thức).	Đồ thị tiến gần đường thẳng đứng khi x tiến gần một giá trị cụ thể x₀.

Những Lỗi Thường Gặp Khi Tìm Tiệm Cận Xiên

Trong quá trình áp dụng cách tìm tiệm cận xiên, người học thường mắc phải một số sai lầm cơ bản sau:

• Không kiểm tra điều kiện a ≠ 0: Nếu a = 0, đó là tiệm cận ngang, không phải tiệm cận xiên.
• Sai sót trong tính toán giới hạn: Đây là lỗi phổ biến nhất, đặc biệt với các biểu thức phức tạp hoặc khi chia đa thức. Cần cẩn thận với các quy tắc L'Hopital hoặc chia cho bậc cao nhất.
• Bỏ qua một phía vô cực: Hàm số có thể có tiệm cận xiên khác nhau khi x→+∞ và x→-∞. Luôn kiểm tra cả hai trường hợp.
• Nhầm lẫn với tiệm cận ngang: Khi bậc tử và mẫu bằng nhau, sẽ có tiệm cận ngang chứ không phải tiệm cận xiên.
• Sử dụng sai phương pháp chia đa thức: Phương pháp chia đa thức chỉ áp dụng trực tiếp cho hàm phân thức hữu tỉ. Đối với các hàm khác (ví dụ: chứa căn thức), bắt buộc phải dùng công thức giới hạn.

Mẹo Nhỏ Để Kiểm Tra Tiệm Cận Xiên Nhanh Chóng

Để củng cố cách tìm tiệm cận xiên và giảm thiểu sai sót, bạn có thể áp dụng một số mẹo sau:

• Ước lượng bậc của hàm số: Đối với hàm phân thức, tiệm cận xiên chỉ tồn tại khi bậc của tử số hơn bậc của mẫu số đúng 1 đơn vị. Đây là một kiểm tra nhanh để loại trừ các trường hợp không có tiệm cận xiên ngay từ đầu.
• Kiểm tra lại phép tính giới hạn: Sau khi tìm được a và b, hãy thay thử một giá trị x rất lớn (hoặc rất nhỏ) vào hàm số f(x) và vào phương trình tiệm cận y = ax + b. Nếu giá trị của f(x) rất gần với ax + b, thì kết quả của bạn có khả năng đúng.
• Sử dụng máy tính bỏ túi hoặc phần mềm: Đối với các bài toán phức tạp, việc sử dụng máy tính bỏ túi có chức năng tính giới hạn hoặc phần mềm đồ thị (như GeoGebra, Desmos) có thể giúp bạn kiểm tra lại kết quả một cách trực quan.

Kết Luận

Việc nắm vững cách tìm tiệm cận xiên là kỹ năng thiết yếu trong môn Toán cao cấp, giúp chúng ta hiểu sâu hơn về hành vi của hàm số và đồ thị của chúng. Bằng cách áp dụng các bước tính giới hạn cho hệ số a và b một cách cẩn thận, cùng với việc kiểm tra các điều kiện tồn tại, bạn hoàn toàn có thể chinh phục được dạng bài tập này. Đừng quên thực hành thường xuyên với nhiều dạng bài tập khác nhau để củng cố kiến thức và tránh những lỗi sai phổ biến nhé!

Các Câu Hỏi Thường Gặp Về Tiệm Cận Xiên (FAQs)

1. Tiệm cận xiên là gì trong môn Toán?

Tiệm cận xiên là một đường thẳng (không phải đường ngang hay đường đứng) mà đồ thị của một hàm số tiến sát đến khi biến số độc lập tiến ra vô cùng (dương hoặc âm vô cùng). Nó cho biết xu hướng của đồ thị tại các miền giá trị lớn của x.

2. Khi nào một hàm số có tiệm cận xiên?

Một hàm số có tiệm cận xiên khi giới hạn của f(x)/x (để tìm 'a') và giới hạn của f(x) - ax (để tìm 'b') đều tồn tại và hữu hạn, với 'a' khác 0. Đối với hàm phân thức, điều kiện là bậc tử lớn hơn bậc mẫu đúng 1 đơn vị.

3. Cách tìm tiệm cận xiên của hàm phân thức nhanh nhất là gì?

Đối với hàm phân thức hữu tỉ có bậc tử số lớn hơn bậc mẫu số đúng 1 đơn vị, bạn có thể thực hiện phép chia đa thức tử cho đa thức mẫu. Phần thương của phép chia (không tính phần dư) chính là phương trình của tiệm cận xiên.

4. Tiệm cận xiên có khác gì tiệm cận ngang không?

Có, tiệm cận xiên có hệ số góc 'a' khác 0 (nghĩa là đường thẳng không song song với trục Ox), trong khi tiệm cận ngang có hệ số góc 'a' bằng 0 (là đường thẳng song song với trục Ox). Chúng mô tả hành vi của đồ thị tại vô cực theo hai hướng khác nhau.

5. Có phải hàm số nào cũng có tiệm cận xiên không?

Không, không phải mọi hàm số đều có tiệm cận xiên. Sự tồn tại của tiệm cận xiên phụ thuộc vào hành vi giới hạn của hàm số khi biến số tiến tới vô cùng, tuân theo các điều kiện đã nêu ở trên.

6. Làm thế nào để kiểm tra kết quả tiệm cận xiên đã tìm được?

Bạn có thể kiểm tra bằng cách thay một giá trị x rất lớn (hoặc rất nhỏ) vào hàm số ban đầu và vào phương trình tiệm cận xiên đã tìm được. Nếu hai giá trị đó rất gần nhau, kết quả của bạn có khả năng đúng. Sử dụng công cụ vẽ đồ thị cũng là cách tốt để xác nhận trực quan.