Khám Phá 'Cho Hình Bình Hành ABCD': Toàn Bộ Kiến Thức Từ A-Z

Khi bạn bắt gặp cụm từ "cho hình bình hành ABCD" trong các bài toán hình học, đó là tín hiệu cho biết bạn đang đối diện với một trong những tứ giác đặc biệt và quan trọng nhất. Hình bình hành là nền tảng của nhiều khái niệm hình học phức tạp hơn, và việc nắm vững các tính chất, dấu hiệu nhận biết cùng công thức liên quan là chìa khóa để giải quyết mọi bài tập. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện, chi tiết nhất về hình bình hành ABCD, từ định nghĩa cơ bản đến các ứng dụng thực tế và cách giải quyết các dạng bài tập phổ biến. Hãy cùng đi sâu tìm hiểu để chinh phục mọi thử thách khi được "cho hình bình hành ABCD" nhé!

Hình Bình Hành ABCD Là Gì? Định Nghĩa Chuẩn Xác

Một tứ giác được gọi là hình bình hành khi nó có các cặp cạnh đối song song. Trong mặt phẳng hình học, nếu bạn cho hình bình hành ABCD, điều đó có nghĩa là bạn đang làm việc với một tứ giác lồi, trong đó cạnh AB song song với cạnh CD, và cạnh AD song song với cạnh BC.

• Định nghĩa cơ bản: Hình bình hành là tứ giác có các cặp cạnh đối song song.
• Ký hiệu: Thường được ký hiệu là ABCD, trong đó các đỉnh được đặt tên theo thứ tự vòng tròn (thuận hoặc ngược chiều kim đồng hồ).
• Cách vẽ: Bạn có thể dễ dàng vẽ một hình bình hành bằng cách vẽ hai cặp đường thẳng song song cắt nhau.

Sự song song của các cạnh đối là tính chất định hình cơ bản nhất, từ đó suy ra mọi tính chất khác của hình bình hành.

Các Tính Chất Của Hình Bình Hành ABCD: Nền Tảng Giải Bài Tập

Việc hiểu rõ các tính chất là cực kỳ quan trọng khi bạn được cho hình bình hành ABCD và cần giải quyết các bài toán liên quan. Có ba nhóm tính chất chính mà một hình bình hành luôn có:

Tính chất về Cạnh của Hình Bình Hành ABCD

Trong một hình bình hành ABCD:

• Các cạnh đối không chỉ song song mà còn bằng nhau. Tức là, AB = CD và AD = BC. Đây là một tính chất rất hữu ích để tính toán độ dài các cạnh còn thiếu hoặc chứng minh các đoạn thẳng bằng nhau.
• Tương tự, các cạnh kề nhau có thể có độ dài khác nhau.

Tính chất về Góc của Hình Bình Hành ABCD

Đối với các góc của một hình bình hành ABCD:

• Các góc đối bằng nhau. Cụ thể, góc A = góc C và góc B = góc D.
• Các góc kề một cạnh thì bù nhau (tổng bằng 180 độ). Ví dụ, góc A + góc B = 180°, góc B + góc C = 180°, v.v. Tính chất này thường được sử dụng để tìm số đo góc hoặc chứng minh các đường thẳng song song.

Tính chất về Đường Chéo của Hình Bình Hành ABCD

Đây là một trong những tính chất mạnh mẽ nhất và thường xuyên được sử dụng khi cho hình bình hành ABCD:

• Hai đường chéo cắt nhau tại trung điểm của mỗi đường. Nếu AC và BD là hai đường chéo cắt nhau tại điểm O, thì O là trung điểm của AC (OA = OC) và O cũng là trung điểm của BD (OB = OD).

"Đường chéo không chỉ kết nối các đỉnh đối diện mà còn là 'chìa khóa' mở ra nhiều tính chất ẩn và cách giải quyết bài toán hiệu quả cho hình bình hành. Khi bạn được cho hình bình hành ABCD và cần chứng minh trung điểm hoặc các đoạn thẳng bằng nhau, hãy nghĩ ngay đến tính chất này."

Dấu Hiệu Nhận Biết Một Tứ Giác Là Hình Bình Hành ABCD

Không phải lúc nào bài toán cũng trực tiếp cho hình bình hành ABCD. Đôi khi, bạn phải tự chứng minh một tứ giác là hình bình hành dựa trên các thông tin đã cho. Dưới đây là 5 dấu hiệu cơ bản để nhận biết một tứ giác là hình bình hành:

1. Tứ giác có các cặp cạnh đối song song. Đây là định nghĩa và cũng là dấu hiệu cơ bản nhất.
2. Tứ giác có các cặp cạnh đối bằng nhau. Nếu AB = CD và AD = BC, thì ABCD là hình bình hành.
3. Tứ giác có các cặp góc đối bằng nhau. Nếu góc A = góc C và góc B = góc D, thì ABCD là hình bình hành.
4. Tứ giác có một cặp cạnh đối song song và bằng nhau. Ví dụ, nếu AB // CD và AB = CD, thì ABCD là hình bình hành. (Đây là dấu hiệu rất phổ biến trong các bài tập chứng minh).
5. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Nếu hai đường chéo AC và BD cắt nhau tại O sao cho OA = OC và OB = OD, thì ABCD là hình bình hành.

Việc ghi nhớ và áp dụng linh hoạt các dấu hiệu này sẽ giúp bạn dễ dàng xác định và làm việc với một tứ giác được cho hình bình hành ABCD trong mọi tình huống.

Công Thức Tính Toán Quan Trọng Cho Hình Bình Hành ABCD

Bên cạnh các tính chất hình học, việc biết cách tính chu vi và diện tích là điều cần thiết khi bạn được cho hình bình hành ABCD trong các bài toán thực tế hoặc ứng dụng.

Công thức tính Chu vi Hình Bình Hành

Chu vi của hình bình hành là tổng độ dài của tất cả các cạnh của nó. Vì các cạnh đối bằng nhau, công thức tính chu vi trở nên đơn giản hơn:

• Nếu độ dài hai cạnh kề nhau của hình bình hành là 'a' và 'b', thì Chu vi (P) = 2 * (a + b).
• Ví dụ: Cho hình bình hành ABCD có cạnh AB = 6cm và cạnh AD = 4cm. Chu vi P = 2 * (6 + 4) = 2 * 10 = 20cm.

Công thức tính Diện tích Hình Bình Hành

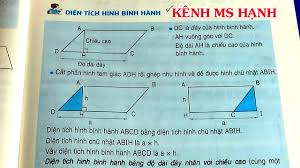
Diện tích của hình bình hành được tính bằng công thức tương tự như hình chữ nhật, nhưng thay chiều rộng bằng chiều cao tương ứng với cạnh đáy:

• Diện tích (S) = độ dài cạnh đáy * chiều cao tương ứng.
• Nếu cạnh đáy là 'a' và chiều cao tương ứng với cạnh đáy đó là 'h', thì S = a * h.
• Lưu ý: Chiều cao là khoảng cách vuông góc từ một đỉnh xuống cạnh đối diện (hoặc đường thẳng chứa cạnh đối diện).

Để dễ hình dung hơn, hãy xem bảng so sánh công thức với các hình quen thuộc:

Hình học	Công thức Chu vi	Công thức Diện tích
Hình Bình Hành ABCD	P = 2(a + b)	S = a * h
Hình Chữ Nhật	P = 2(dài + rộng)	S = dài * rộng
Hình Vuông	P = 4 * cạnh	S = cạnh * cạnh

Các Dạng Bài Tập Thường Gặp Khi "Cho Hình Bình Hành ABCD"

Khi bạn đã nắm vững định nghĩa, tính chất và dấu hiệu nhận biết, việc áp dụng vào giải bài tập là bước tiếp theo. Các bài toán về cho hình bình hành ABCD rất đa dạng, nhưng có thể chia thành một số dạng cơ bản:

Chứng minh một Tứ Giác là Hình Bình Hành

Đây là dạng bài tập cơ bản nhưng quan trọng. Bạn sẽ được cho một tứ giác ABCD với một số thông tin và yêu cầu chứng minh nó là hình bình hành. Bạn cần vận dụng 5 dấu hiệu nhận biết đã nêu ở trên.

• Ví dụ: "Cho tứ giác ABCD có AB // CD và AB = CD. Chứng minh ABCD là hình bình hành." (Sử dụng dấu hiệu 4).

Tính Độ Dài Cạnh, Góc, Chu vi, Diện Tích

Dạng bài này yêu cầu bạn áp dụng trực tiếp các tính chất về cạnh, góc và các công thức chu vi, diện tích. Bạn có thể cần sử dụng thêm định lý Py-ta-go hoặc các kiến thức về tam giác nếu có chiều cao hoặc đường chéo được cho.

• Ví dụ: "Cho hình bình hành ABCD có góc A = 70 độ. Tính các góc còn lại." (Sử dụng tính chất góc đối và góc kề bù).
• Ví dụ: "Cho hình bình hành ABCD có độ dài đường chéo AC = 10cm, BD = 8cm và chúng cắt nhau tại O. Tính độ dài OA và OB." (Sử dụng tính chất đường chéo cắt nhau tại trung điểm).

Ứng Dụng Tính Chất Đường Chéo và Tâm Đối Xứng

Các bài toán nâng cao hơn có thể yêu cầu bạn chứng minh các điểm là trung điểm, các đường thẳng song song, hoặc tìm tâm đối xứng của hình bình hành (chính là giao điểm của hai đường chéo).

• Đây thường là bước đệm để giải quyết các bài toán liên quan đến véc-tơ hoặc tọa độ trong mặt phẳng.

Những Loại Hình Đặc Biệt Của 'Cho Hình Bình Hành ABCD'

Hình bình hành là một khái niệm rộng, và trong đó, có ba loại hình đặc biệt mà mỗi loại lại có thêm những tính chất riêng biệt, nhưng tất cả đều là hình bình hành:

• Hình chữ nhật: Là hình bình hành có một góc vuông (suy ra tất cả các góc đều vuông). Đặc biệt, hai đường chéo của hình chữ nhật bằng nhau.
• Hình thoi: Là hình bình hành có hai cạnh kề bằng nhau (suy ra tất cả các cạnh đều bằng nhau). Đặc biệt, hai đường chéo của hình thoi vuông góc với nhau và là đường phân giác của các góc.
• Hình vuông: Là hình bình hành vừa có một góc vuông vừa có hai cạnh kề bằng nhau (tức là vừa là hình chữ nhật vừa là hình thoi). Hình vuông có đầy đủ các tính chất của cả hình chữ nhật và hình thoi.

Sự phân loại này rất quan trọng để bạn không nhầm lẫn các tính chất riêng biệt của từng loại hình khi được cho hình bình hành ABCD mà có thêm điều kiện phụ.

Tầm Quan Trọng Của Việc Nắm Vững 'Cho Hình Bình Hành ABCD' Trong Học Tập và Thực Tiễn

Hiểu sâu về hình bình hành không chỉ giúp bạn đạt điểm cao trong môn toán mà còn phát triển tư duy logic, khả năng suy luận hình học. Cụ thể:

• Nền tảng cho hình học cao cấp: Các tính chất của hình bình hành là cơ sở để nghiên cứu về hình học không gian (khối hộp chữ nhật, hình lập phương), véc-tơ, và các phép biến hình.
• Phát triển kỹ năng giải quyết vấn đề: Việc giải các bài toán "cho hình bình hành ABCD" đòi hỏi bạn phải phân tích đề bài, lựa chọn phương pháp phù hợp và trình bày lời giải một cách mạch lạc.
• Ứng dụng trong thực tiễn (mặc dù gián tiếp): Kiến thức về hình học phẳng, bao gồm hình bình hành, được ứng dụng trong nhiều lĩnh vực như kiến trúc (thiết kế mái nhà, cửa sổ), kỹ thuật (cấu trúc cầu, máy móc), thiết kế đồ họa, và nghệ thuật.

Mỗi khi bạn được cho hình bình hành ABCD, hãy xem đó là một cơ hội để rèn luyện và củng cố kiến thức hình học của mình.

Kết Luận

Từ định nghĩa đến các tính chất, dấu hiệu nhận biết, công thức tính toán và các dạng bài tập, chúng ta đã cùng nhau khám phá toàn bộ thế giới của hình bình hành. Việc nắm vững các khái niệm cơ bản khi cho hình bình hành ABCD là điều kiện tiên quyết để bạn có thể tự tin giải quyết mọi bài toán liên quan và phát triển hơn nữa trong môn hình học. Hãy luôn luyện tập và áp dụng linh hoạt các kiến thức đã học để biến những khái niệm trừu tượng thành công cụ giải quyết vấn đề hiệu quả.

Nếu bạn gặp bất kỳ bài toán nào có cụm từ "cho hình bình hành ABCD" và cảm thấy bối rối, hãy nhớ lại những kiến thức trong bài viết này. Thực hành thường xuyên sẽ giúp bạn trở thành chuyên gia về hình bình hành!

Câu Hỏi Thường Gặp (FAQs) Về Hình Bình Hành ABCD

1. Hình bình hành ABCD là gì một cách đơn giản nhất?
Hình bình hành ABCD là một tứ giác đặc biệt có hai cặp cạnh đối song song với nhau. Điều này có nghĩa là cạnh AB song song với CD, và cạnh AD song song với BC, tạo nên một hình dạng cân đối.

2. Tại sao đường chéo lại quan trọng khi 'cho hình bình hành ABCD'?
Đường chéo rất quan trọng vì chúng cắt nhau tại trung điểm của mỗi đường. Tính chất này là nền tảng để chứng minh nhiều mối quan hệ khác trong hình, giúp bạn giải quyết các bài toán về trung điểm, đoạn thẳng bằng nhau khi được cho hình bình hành ABCD.

3. Khi nào thì một tứ giác được coi là hình bình hành ABCD?
Một tứ giác được coi là hình bình hành ABCD khi nó thỏa mãn một trong các dấu hiệu: các cặp cạnh đối song song, các cặp cạnh đối bằng nhau, các cặp góc đối bằng nhau, một cặp cạnh đối song song và bằng nhau, hoặc hai đường chéo cắt nhau tại trung điểm mỗi đường.

4. Làm thế nào để tính diện tích khi 'cho hình bình hành ABCD' có chiều cao và cạnh đáy?
Để tính diện tích hình bình hành ABCD, bạn chỉ cần nhân độ dài cạnh đáy với chiều cao tương ứng của cạnh đó. Công thức là S = a * h, trong đó 'a' là độ dài cạnh đáy và 'h' là chiều cao vuông góc từ cạnh đối xuống cạnh đáy đó.

5. Có nên nhầm lẫn hình bình hành ABCD với hình chữ nhật không?
Không nên nhầm lẫn. Mặc dù hình chữ nhật là một dạng đặc biệt của hình bình hành (có thêm tính chất góc vuông và đường chéo bằng nhau), nhưng không phải mọi hình bình hành đều là hình chữ nhật. Hình bình hành tổng quát không yêu cầu các góc phải vuông.

6. Ai là người đầu tiên nghiên cứu về hình bình hành trong lịch sử toán học?
Khái niệm về hình bình hành và các tính chất của nó đã được nghiên cứu từ thời Hy Lạp cổ đại, đặc biệt trong các tác phẩm của Euclid. Ông đã hệ thống hóa nhiều định lý cơ bản về hình học, đặt nền móng cho việc hiểu rõ các hình dạng như khi chúng ta được cho hình bình hành ABCD ngày nay.