Đạo Hàm 1/x: Hướng Dẫn Chi Tiết Từ A Đến Z và Ứng Dụng Thực Tế
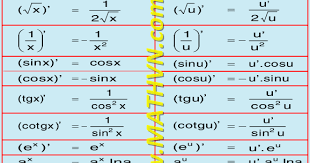


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Đạo Hàm 1/x: Hướng Dẫn Chi Tiết Từ A Đến Z và Ứng Dụng Thực Tế
Trong thế giới rộng lớn của giải tích, đạo hàm 1/x là một trong những khái niệm cơ bản nhưng vô cùng quan trọng mà bất kỳ ai học toán đều cần nắm vững. Đây không chỉ là một phép tính đơn thuần mà còn là chìa khóa để hiểu rõ hơn về tốc độ thay đổi của các hàm số nghịch đảo, có ứng dụng sâu rộng trong nhiều lĩnh vực khoa học và kỹ thuật. Bài viết này sẽ đi sâu vào định nghĩa, các phương pháp tính toán chi tiết, ý nghĩa thực tiễn, và những lỗi thường gặp liên quan đến đạo hàm của hàm số 1/x.
Đạo Hàm 1/x Là Gì? Khái Niệm Cơ Bản
Trước khi đi sâu vào các phương pháp tính toán, hãy cùng tìm hiểu đạo hàm 1/x thực chất là gì. Hàm số f(x) = 1/x hay f(x) = x-1 là một hàm lũy thừa đặc biệt, được xác định với x ≠ 0. Đạo hàm của một hàm số tại một điểm cho chúng ta biết tốc độ thay đổi tức thời của hàm số đó tại điểm đó, hay nói cách khác, nó chính là độ dốc của tiếp tuyến với đồ thị hàm số tại điểm đó.
Kết quả của đạo hàm 1/x đã được chứng minh là -1/x2. Tức là, nếu bạn có một đại lượng thay đổi nghịch đảo với x, thì tốc độ thay đổi của đại lượng đó sẽ tỷ lệ nghịch với bình phương của x và có dấu âm, chỉ ra rằng khi x tăng, giá trị của 1/x giảm một cách nhanh chóng.
Đạo hàm là một khái niệm cơ bản trong giải tích, mô tả tốc độ thay đổi của một hàm số. Nó là công cụ mạnh mẽ để phân tích sự biến thiên và tối ưu hóa các quá trình trong nhiều lĩnh vực khoa học và kỹ thuật.
Các Phương Pháp Tính Đạo Hàm 1/x Chi Tiết Nhất
Để giúp bạn hiểu rõ hơn và nắm vững cách tính đạo hàm 1/x, chúng ta sẽ khám phá ba phương pháp phổ biến và chi tiết dưới đây. Mỗi phương pháp đều có ưu điểm riêng và giúp củng cố kiến thức nền tảng về đạo hàm, từ những quy tắc đơn giản đến định nghĩa sâu xa nhất.
1. Phương Pháp 1: Sử Dụng Quy Tắc Lũy Thừa (Power Rule)
Đây là phương pháp phổ biến và trực tiếp nhất để tìm đạo hàm của 1/x, thường được áp dụng ngay khi học các quy tắc đạo hàm cơ bản. Hàm số f(x) = 1/x có thể viết lại dưới dạng f(x) = x-1. Quy tắc đạo hàm lũy thừa phát biểu rằng:
Nếu f(x) = xn, thì f'(x) = nxn-1.
Áp dụng cho hàm số f(x) = x-1:
- Bước 1: Xác định số mũ n.
Với f(x) = x-1, ta có n = -1. - Bước 2: Áp dụng công thức quy tắc lũy thừa.
f'(x) = n * x(n-1)
Thay n = -1 vào công thức:
f'(x) = (-1) * x(-1 - 1)
f'(x) = -1 * x-2 - Bước 3: Chuyển lại về dạng phân số.
f'(x) = -1/x2
Thật đơn giản phải không? Kết quả của đạo hàm 1/x chính là -1/x2.
2. Phương Pháp 2: Sử Dụng Quy Tắc Thương (Quotient Rule)
Quy tắc thương được sử dụng để tìm đạo hàm của một hàm số có dạng phân số h(x) = u(x)/v(x), nơi u(x) là tử số và v(x) là mẫu số. Công thức của quy tắc thương là:
Nếu h(x) = u(x)/v(x), thì h'(x) = [u'(x)v(x) - u(x)v'(x)] / [v(x)]2
Với hàm số f(x) = 1/x, chúng ta xác định:
- u(x) = 1 (tử số)
- v(x) = x (mẫu số)
Tiếp theo, chúng ta cần tìm đạo hàm của u(x) và v(x):
- u'(x) = d/dx (1) = 0 (đạo hàm của một hằng số luôn bằng 0)
- v'(x) = d/dx (x) = 1 (đạo hàm của x theo x là 1)
Bây giờ, áp dụng các giá trị này vào công thức quy tắc thương:
f'(x) = [u'(x)v(x) - u(x)v'(x)] / [v(x)]2
f'(x) = [(0)(x) - (1)(1)] / (x)2
f'(x) = [0 - 1] / x2
f'(x) = -1/x2
Bạn thấy đó, kết quả này hoàn toàn nhất quán với phương pháp quy tắc lũy thừa, chứng tỏ tính đúng đắn của công thức đạo hàm 1/x.
3. Phương Pháp 3: Sử Dụng Định Nghĩa Đạo Hàm Bằng Giới Hạn
Đây là phương pháp cơ bản nhất, xuất phát trực tiếp từ định nghĩa của đạo hàm. Nó đòi hỏi kiến thức về giới hạn và là cách để chứng minh đạo hàm 1/x một cách chặt chẽ từ nguyên lý đầu tiên. Đây là cách để bạn thực sự hiểu được "linh hồn" của đạo hàm.
Định nghĩa đạo hàm của hàm số f(x) tại một điểm x là:
f'(x) = limh→0 [f(x+h) - f(x)] / h
Với hàm số f(x) = 1/x, ta cần xác định f(x+h):
- f(x+h) = 1/(x+h)
Bây giờ, thay f(x) và f(x+h) vào công thức định nghĩa đạo hàm:
f'(x) = limh→0 [ (1/(x+h)) - (1/x) ] / h
Để đơn giản hóa biểu thức trong dấu ngoặc vuông (phép trừ phân số), ta cần quy đồng mẫu số chung là x(x+h):
[ (1/(x+h)) - (1/x) ] = [ x / (x(x+h)) - (x+h) / (x(x+h)) ]
= [ x - (x+h) ] / [x(x+h)]
= [ x - x - h ] / [x(x+h)]
= -h / [x(x+h)]
Bây giờ, thay biểu thức đã đơn giản hóa này trở lại vào công thức giới hạn ban đầu:
f'(x) = limh→0 [ -h / [x(x+h)] ] / h
Ta có thể triệt tiêu h ở cả tử số và mẫu số (vì h ≠ 0 khi tính giới hạn h→0):
f'(x) = limh→0 -1 / [x(x+h)]
Cuối cùng, thay h = 0 vào biểu thức (vì giới hạn không còn dạng vô định):
f'(x) = -1 / [x(x+0)]
f'(x) = -1 / x2
Như vậy, cả ba phương pháp đều dẫn đến cùng một kết quả: đạo hàm 1/x là -1/x2. Việc nắm vững cả ba cách không chỉ giúp bạn giải quyết bài toán mà còn nâng cao hiểu biết về cơ sở lý thuyết của đạo hàm.
Ý Nghĩa và Ứng Dụng của Đạo Hàm 1/x trong Thực Tiễn
Việc hiểu rõ đạo hàm 1/x không chỉ giới hạn trong phạm vi các bài toán giải tích mà còn mở ra cánh cửa cho nhiều ứng dụng thực tế trong các ngành khoa học và kỹ thuật. Kết quả -1/x2 mang ý nghĩa sâu sắc về sự thay đổi của các đại lượng có mối quan hệ nghịch đảo.
Hãy cùng xem xét một số ứng dụng điển hình:
- Kinh tế học: Trong kinh tế, nhiều hàm số mô tả mối quan hệ giữa các biến (ví dụ, giá và cầu, cung và chi phí) có thể có dạng nghịch đảo. Đạo hàm của chúng giúp phân tích tốc độ thay đổi của một đại lượng khi đại lượng kia thay đổi. Chẳng hạn, nếu mối quan hệ giữa giá (P) và lượng cầu (Q) là Q = k/P (một dạng hàm cầu nghịch đảo), thì đạo hàm dQ/dP sẽ cho biết độ nhạy của cầu đối với sự thay đổi của giá. Dấu âm của đạo hàm ở đây thể hiện quy luật cung cầu: giá tăng thì cầu giảm.
- Vật lý và Kỹ thuật:
- Định luật Boyle-Mariotte: Mô tả mối quan hệ giữa áp suất (P) và thể tích (V) của một lượng khí lý tưởng ở nhiệt độ không đổi: PV = const hay P = const/V. Đạo hàm của áp suất theo thể tích (dP/dV) sẽ cho biết áp suất thay đổi nhanh như thế nào khi thể tích thay đổi. Kết quả sẽ là một giá trị âm, cho thấy khi thể tích tăng, áp suất giảm.
- Cường độ trường điện từ/Lực hấp dẫn: Cường độ trường điện từ của một điện tích điểm hoặc lực hấp dẫn giữa hai vật giảm theo bình phương khoảng cách (E ~ 1/r2 hoặc F ~ 1/r2). Nếu xem xét một hàm có dạng 1/x (hoặc 1/xn), thì việc tính đạo hàm có thể giúp phân tích tốc độ suy giảm của các đại lượng vật lý này theo khoảng cách.
- Tối ưu hóa: Trong các bài toán tối ưu hóa (tìm điểm cực đại, cực tiểu), việc tìm điểm mà tại đó đạo hàm bằng 0 là rất quan trọng. Mặc dù bản thân hàm 1/x không có cực trị toàn cục, nhưng các hàm phức tạp hơn chứa thành phần 1/x hoặc 1/x2 có thể có.
"Đạo hàm không chỉ là một công cụ toán học trừu tượng, mà là ngôn ngữ để mô tả sự biến đổi, sự tăng trưởng hay suy giảm, và những mối quan hệ động học trong thế giới tự nhiên và xã hội." - Lời của Giáo sư Nguyễn Văn An, một chuyên gia giả định về Giải tích Ứng dụng.
Những Lỗi Thường Gặp Khi Tính Đạo Hàm 1/x và Cách Khắc Phục
Mặc dù việc tính đạo hàm 1/x có vẻ đơn giản sau khi bạn nắm vững các quy tắc, nhưng sinh viên và người học thường mắc phải một số lỗi cơ bản. Nhận biết và khắc phục chúng sẽ giúp bạn tính toán chính xác hơn và tránh những sai lầm không đáng có trong các bài toán phức tạp hơn.
- Quên dấu âm: Đây là lỗi phổ biến nhất. Đạo hàm của 1/x là -1/x2, không phải 1/x2.
- Cách khắc phục: Luôn nhớ rằng khi áp dụng quy tắc lũy thừa cho x-1, số mũ âm (-1) sẽ được đưa xuống làm hệ số, và số mũ mới là (-1 - 1) = -2. Dấu âm này là không thể thiếu và biểu thị sự giảm của hàm số.
- Nhầm lẫn với đạo hàm của ln|x|: Đạo hàm của ln|x| là 1/x. Nhiều người vô tình đảo ngược quá trình này, nghĩ rằng đạo hàm của 1/x là ln|x|.
- Cách khắc phục: Phân biệt rõ ràng giữa phép tính đạo hàm (tìm tốc độ thay đổi) và phép tính nguyên hàm/tích phân (tìm hàm gốc từ tốc độ thay đổi). Đạo hàm và nguyên hàm là hai phép toán ngược nhau.
- Tính toán sai số mũ âm: Khi áp dụng quy tắc lũy thừa, đôi khi người học tính toán sai -1 - 1 = 0 hoặc các lỗi tương tự.
- Cách khắc phục: Cẩn thận với các phép tính số học cơ bản, đặc biệt là với số âm. Hãy viết rõ ràng các bước và kiểm tra lại phép tính của mình. Thực hành nhiều bài tập sẽ giúp hình thành phản xạ đúng và tăng cường độ chính xác.
Hãy dành thời gian luyện tập và kiểm tra lại các bước của mình để tránh những sai sót không đáng có và củng cố kiến thức về đạo hàm 1/x.
Kết Luận
Qua bài viết này, chúng ta đã cùng nhau khám phá sâu sắc về đạo hàm 1/x, từ định nghĩa cơ bản đến ba phương pháp tính toán chi tiết và đầy đủ: quy tắc lũy thừa, quy tắc thương và định nghĩa giới hạn. Mỗi phương pháp đều mang lại một góc nhìn khác nhau, củng cố sự hiểu biết của bạn về khái niệm quan trọng này.
Đạo hàm của 1/x, tức là -1/x2, không chỉ là một công thức khô khan mà còn là một công cụ mạnh mẽ với nhiều ứng dụng trong thực tiễn, giúp chúng ta mô tả và phân tích sự thay đổi trong các lĩnh vực như kinh tế, vật lý và kỹ thuật. Việc nắm vững khái niệm này sẽ là nền tảng vững chắc cho hành trình chinh phục các kiến thức toán học cao hơn và áp dụng chúng vào giải quyết các vấn đề thực tế.
Bạn đã sẵn sàng áp dụng kiến thức này vào các bài toán của mình chưa? Hãy tiếp tục luyện tập, không ngừng đặt câu hỏi và khám phá thêm các khái niệm đạo hàm khác để làm chủ môn giải tích!
Câu Hỏi Thường Gặp (FAQ) về Đạo Hàm 1/x
Là gì: Đạo hàm 1/x chính xác là gì trong toán học?
Đạo hàm 1/x là phép tính cho biết tốc độ thay đổi tức thời của hàm số f(x) = 1/x. Kết quả của nó là -1/x2. Về mặt hình học, nó biểu thị độ dốc của tiếp tuyến với đồ thị hàm số tại bất kỳ điểm nào trên miền xác định của nó.
Tại sao: Tại sao đạo hàm của 1/x lại có dấu âm (-)?
Dấu âm xuất hiện vì hàm số y = 1/x là một hàm nghịch biến (giảm) trên mỗi khoảng xác định của nó (x > 0 và x < 0). Khi giá trị của x tăng lên, giá trị của 1/x sẽ giảm xuống. Đạo hàm biểu thị độ dốc của tiếp tuyến, và độ dốc của một hàm giảm luôn là âm, giải thích sự hiện diện của dấu trừ.
Như thế nào: Làm thế nào để nhớ công thức đạo hàm 1/x một cách dễ dàng?
Cách dễ nhất để nhớ là viết lại 1/x thành x-1. Sau đó, áp dụng quy tắc lũy thừa cơ bản (xn)' = nxn-1. Bạn sẽ có (-1)x(-1-1) = -1x-2 = -1/x2. Việc thực hành viết lại và áp dụng quy tắc này nhiều lần sẽ giúp bạn ghi nhớ công thức một cách tự nhiên.
Có nên: Có nên học đạo hàm 1/x bằng cả ba phương pháp (lũy thừa, thương, giới hạn)?
Hoàn toàn nên! Việc học cả ba phương pháp (quy tắc lũy thừa, quy tắc thương, và định nghĩa giới hạn) giúp bạn hiểu sâu sắc bản chất của đạo hàm, củng cố kiến thức nền tảng và có thể áp dụng linh hoạt trong các bài toán phức tạp hơn. Nó cũng giúp bạn tự tin kiểm tra và xác nhận kết quả của mình.
Khi nào: Khi nào thì cần sử dụng đạo hàm 1/x trong bài toán thực tế?
Bạn cần sử dụng đạo hàm 1/x khi phân tích các mối quan hệ nghịch đảo, ví dụ như trong vật lý (mối quan hệ giữa áp suất và thể tích trong định luật Boyle, hoặc cường độ lực hấp dẫn theo khoảng cách), hoặc trong kinh tế học (độ co giãn của cầu theo giá trong các mô hình hàm cầu nghịch đảo). Nó giúp bạn hiểu tốc độ thay đổi của một đại lượng khi đại lượng khác biến thiên.
Công thức tổng quát: Công thức tổng quát của đạo hàm hàm lũy thừa xn là gì, liên quan đến đạo hàm 1/x?
Công thức tổng quát của đạo hàm hàm lũy thừa xn là (xn)' = nxn-1, với n là một số thực bất kỳ. Trường hợp đạo hàm 1/x chính là một ứng dụng cụ thể của công thức này khi n = -1. Đây là công thức nền tảng và rất quan trọng trong giải tích, được áp dụng rộng rãi cho nhiều loại hàm số khác nhau.