Diện Tích Hình Thoi: Công Thức, Cách Tính & Ứng Dụng Từ A-Z

Hình học là một nhánh thú vị của toán học, nơi chúng ta khám phá vẻ đẹp và tính chất của các hình khối. Trong số đó, hình thoi nổi bật với những đặc điểm đối xứng và ứng dụng đa dạng. Một trong những khái niệm quan trọng nhất khi làm việc với hình thoi chính là diện tích hình thoi – đại lượng biểu thị độ lớn của mặt phẳng mà hình thoi đó chiếm giữ. Hiểu rõ cách tính diện tích hình thoi không chỉ giúp bạn giải quyết các bài toán học mà còn ứng dụng trong nhiều lĩnh vực thực tế. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về công thức, cách tính và những ứng dụng bất ngờ của diện tích hình thoi trong đời sống.

Hình Thoi Là Gì? Đặc Điểm Nổi Bật Của Hình Thoi

Trước khi đi sâu vào các công thức tính diện tích hình thoi, chúng ta hãy cùng nhắc lại định nghĩa và các tính chất cơ bản của hình này. Hình thoi là một tứ giác có bốn cạnh bằng nhau. Nó cũng là một dạng đặc biệt của hình bình hành.

Các đặc điểm quan trọng của hình thoi bao gồm:

• Bốn cạnh bằng nhau: Đây là dấu hiệu nhận biết cơ bản nhất của hình thoi.

• Các góc đối diện bằng nhau: Tương tự như hình bình hành.

• Hai đường chéo vuông góc với nhau: Đây là một tính chất cực kỳ quan trọng và là nền tảng cho công thức tính diện tích hình thoi phổ biến nhất.

• Hai đường chéo là đường phân giác của các góc: Mỗi đường chéo chia đôi góc mà nó đi qua.

• Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Giống như hình bình hành.

• Hình thoi có hai trục đối xứng chính là hai đường chéo của nó.

Công Thức Tính Diện Tích Hình Thoi Cơ Bản Nhất

Có nhiều cách để tính diện tích hình thoi tùy thuộc vào dữ kiện bạn có. Tuy nhiên, công thức qua hai đường chéo là phổ biến và dễ nhớ nhất.

Công thức diện tích hình thoi qua hai đường chéo

Đây là công thức được sử dụng rộng rãi và thường xuyên nhất trong các bài toán về hình thoi. Để tính diện tích hình thoi, bạn chỉ cần biết độ dài của hai đường chéo.

Công thức:

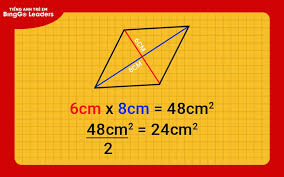
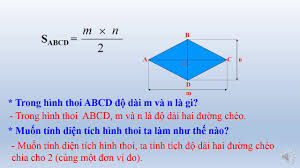
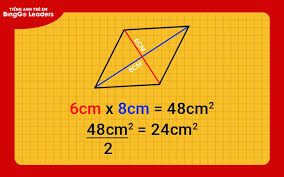
S = (d1 * d2) / 2

Trong đó:

• S là diện tích hình thoi.

• d1 là độ dài của đường chéo thứ nhất.

• d2 là độ dài của đường chéo thứ hai.

Giải thích: Bạn có thể hình dung rằng hai đường chéo của hình thoi chia hình thoi thành bốn tam giác vuông bằng nhau. Khi ghép các tam giác này lại, bạn có thể tạo thành một hình chữ nhật có chiều dài và chiều rộng lần lượt bằng độ dài của hai đường chéo, và diện tích hình thoi chính bằng một nửa diện tích hình chữ nhật đó.

Ví dụ minh họa:

Một hình thoi có đường chéo thứ nhất dài 8 cm và đường chéo thứ hai dài 10 cm. Tính diện tích hình thoi đó.

1. Xác định độ dài hai đường chéo: d1 = 8 cm, d2 = 10 cm.

2. Áp dụng công thức: S = (d1 * d2) / 2

3. Thực hiện phép tính: S = (8 * 10) / 2 = 80 / 2 = 40 cm².

Vậy, diện tích hình thoi là 40 cm².

Công thức diện tích hình thoi qua cạnh và chiều cao

Giống như hình bình hành, hình thoi cũng có thể được tính diện tích dựa vào độ dài cạnh đáy và chiều cao tương ứng.

Công thức:

S = a * h

Trong đó:

• S là diện tích hình thoi.

• a là độ dài một cạnh của hình thoi (vì tất cả các cạnh đều bằng nhau).

• h là chiều cao từ một đỉnh xuống cạnh đối diện (đường vuông góc từ đỉnh đó xuống cạnh).

Ví dụ minh họa:

Một hình thoi có độ dài cạnh là 6 dm và chiều cao tương ứng là 4 dm. Tính diện tích hình thoi đó.

1. Xác định độ dài cạnh và chiều cao: a = 6 dm, h = 4 dm.

2. Áp dụng công thức: S = a * h

3. Thực hiện phép tính: S = 6 * 4 = 24 dm².

Vậy, diện tích hình thoi là 24 dm².

Công thức diện tích hình thoi qua cạnh và góc

Đối với những bài toán nâng cao hơn, bạn có thể cần đến công thức tính diện tích hình thoi khi biết độ dài một cạnh và một góc bất kỳ của nó.

Công thức:

S = a² * sin(α)

Trong đó:

• S là diện tích hình thoi.

• a là độ dài một cạnh của hình thoi.

• α (alpha) là số đo của một góc bất kỳ của hình thoi (có thể là góc nhọn hoặc góc tù).

• sin(α) là giá trị sin của góc đó.

Lưu ý: Công thức này yêu cầu kiến thức về hàm lượng giác (sin), thường được học ở cấp trung học cơ sở trở lên.

Ví Dụ Thực Tế Về Cách Tính Diện Tích Hình Thoi

Để củng cố kiến thức về diện tích hình thoi, hãy cùng xem xét một số ví dụ thực tế đa dạng hơn.

Ví dụ 1: Tính diện tích một mảnh vườn hình thoi

Gia đình bạn có một mảnh vườn nhỏ hình thoi để trồng rau. Bạn đo được một đường chéo dài 12 mét và đường chéo còn lại dài 9 mét. Hỏi diện tích mảnh vườn là bao nhiêu?

Giải:

Áp dụng công thức S = (d1 * d2) / 2:

• d1 = 12 m

• d2 = 9 m

• S = (12 * 9) / 2 = 108 / 2 = 54 m²

Vậy, diện tích mảnh vườn là 54 mét vuông. Điều này giúp bạn ước tính lượng hạt giống hoặc phân bón cần thiết.

Ví dụ 2: Tìm đường chéo còn lại khi biết diện tích và một đường chéo

Một tấm kính trang trí hình thoi có diện tích 72 cm². Nếu một đường chéo của tấm kính dài 16 cm, hãy tìm độ dài đường chéo còn lại.

Giải:

Từ công thức S = (d1 * d2) / 2, ta có thể suy ra d2 = (2 * S) / d1.

• S = 72 cm²

• d1 = 16 cm

• d2 = (2 * 72) / 16 = 144 / 16 = 9 cm

Vậy, độ dài đường chéo còn lại của tấm kính là 9 cm.

Ví dụ 3: Bài toán liên quan đến chu vi và diện tích hình thoi

Một miếng gỗ hình thoi có chu vi 20 cm. Biết chiều cao tương ứng với một cạnh là 4 cm. Tính diện tích miếng gỗ đó.

Giải:

Vì hình thoi có 4 cạnh bằng nhau, từ chu vi ta có thể tìm được độ dài một cạnh:

• Độ dài một cạnh a = Chu vi / 4 = 20 / 4 = 5 cm.

• Chiều cao h = 4 cm.

Áp dụng công thức S = a * h:

• S = 5 * 4 = 20 cm²

Vậy, diện tích miếng gỗ là 20 cm².

Ứng Dụng Của Diện Tích Hình Thoi Trong Đời Sống Và Học Tập

Việc học và hiểu về diện tích hình thoi không chỉ giới hạn trong sách vở mà còn có rất nhiều ứng dụng thực tế:

• Kiến trúc và xây dựng: Các kiến trúc sư, kỹ sư thường xuyên sử dụng các hình dạng hình học để thiết kế các công trình. Hình thoi có thể xuất hiện trong thiết kế cửa sổ, gạch lát sàn, hoặc các hoa văn trang trí, yêu cầu tính toán diện tích để ước lượng vật liệu.

• Thiết kế nội thất và trang trí: Trong thiết kế nội thất, hình thoi được dùng làm họa tiết trên thảm, rèm cửa, giấy dán tường hay các đồ vật trang trí. Tính diện tích giúp xác định kích thước, số lượng vật liệu cần thiết.

• Nghệ thuật và thủ công: Những người làm đồ thủ công, thợ may, hay nghệ sĩ có thể tạo ra các sản phẩm có hình thoi, như chăn vá, đồ trang sức. Việc tính diện tích là cần thiết để cắt vải, giấy hoặc vật liệu khác một cách chính xác.

• Thiết kế đồ họa: Trong lĩnh vực thiết kế đồ họa, hình thoi được sử dụng làm yếu tố thiết kế trong logo, biểu tượng, hoặc các mẫu trang web. Hiểu về diện tích giúp căn chỉnh và tạo ra bố cục cân đối.

• Toán học và giáo dục: Tất nhiên, việc học về diện tích hình thoi là một phần không thể thiếu trong chương trình giáo dục toán học từ cấp tiểu học đến trung học, giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề.

Mẹo Nhớ Công Thức Diện Tích Hình Thoi Dễ Dàng

Để ghi nhớ công thức tính diện tích hình thoi một cách hiệu quả, bạn có thể áp dụng một số mẹo nhỏ sau:

• Liên hệ với hình chữ nhật: Hãy nhớ rằng diện tích hình thoi bằng một nửa diện tích hình chữ nhật được tạo bởi hai đường chéo của nó. Tức là (d1 * d2) / 2.

• Nhớ câu thần chú: "Nửa tích hai đường chéo" – đây là cách dễ nhất để ghi nhớ công thức cơ bản.

• Vẽ sơ đồ: Tự tay vẽ một hình thoi, vẽ hai đường chéo, sau đó thử ghép các tam giác vuông để tạo thành một hình chữ nhật. Việc hình dung trực quan sẽ giúp bạn khắc sâu công thức.

• Thực hành thường xuyên: Cách tốt nhất để ghi nhớ là làm bài tập và áp dụng công thức vào các tình huống khác nhau. Càng thực hành nhiều, công thức sẽ càng trở nên quen thuộc.

"Toán học không chỉ là những con số và công thức, mà là ngôn ngữ để mô tả vũ trụ." - Theo Galilei. Hãy biến việc học diện tích hình thoi thành một trải nghiệm khám phá thú vị!

Kết Luận

Qua bài viết này, hy vọng bạn đã có cái nhìn rõ ràng và đầy đủ về diện tích hình thoi, từ định nghĩa cơ bản, các công thức tính toán khác nhau, cho đến những ví dụ minh họa và ứng dụng thực tiễn trong cuộc sống. Nắm vững kiến thức này không chỉ giúp bạn tự tin giải quyết các bài toán hình học mà còn mở rộng khả năng quan sát và ứng dụng toán học vào thế giới xung quanh. Hãy tiếp tục thực hành và khám phá thêm nhiều điều thú vị khác về các hình học nhé!

Câu Hỏi Thường Gặp Về Diện Tích Hình Thoi (FAQ)

1. Diện tích hình thoi là gì và có ý nghĩa như thế nào?
Diện tích hình thoi là phép đo không gian hai chiều mà hình thoi đó chiếm trên một mặt phẳng. Nó có ý nghĩa quan trọng trong việc tính toán vật liệu cần thiết cho các thiết kế, xây dựng, hoặc đơn giản là để hiểu về độ lớn của một hình dạng cụ thể trong toán học và đời sống.

2. Làm thế nào để tính diện tích hình thoi khi chỉ biết một đường chéo và một cạnh?
Khi chỉ biết một đường chéo và một cạnh, bạn có thể dùng định lý Pytago để tìm một nửa đường chéo còn lại (vì các đường chéo vuông góc và cắt nhau tại trung điểm), sau đó áp dụng công thức S = (d1 * d2) / 2. Cách khác là tìm chiều cao bằng cách sử dụng công thức Heron hoặc lượng giác.

3. Tại sao công thức diện tích hình thoi lại liên quan đến tích hai đường chéo?
Công thức này xuất phát từ việc hình thoi có thể được xem là một nửa diện tích của hình chữ nhật có kích thước bằng hai đường chéo của nó. Khi bạn nhân hai đường chéo và chia đôi, bạn sẽ có được diện tích chính xác của hình thoi.

4. Có nên áp dụng công thức diện tích hình thoi qua sin góc trong bài tập cấp 1 không?
Không nên. Công thức diện tích hình thoi qua sin góc (S = a² * sin(α)) liên quan đến hàm lượng giác và thường được dạy ở cấp trung học cơ sở trở lên. Đối với học sinh tiểu học, hãy tập trung vào công thức S = (d1 * d2) / 2 hoặc S = a * h.

5. Diện tích hình thoi khác gì so với diện tích hình vuông?
Hình vuông là một trường hợp đặc biệt của hình thoi (khi hai đường chéo bằng nhau và vuông góc nhau, hoặc khi tất cả các góc bằng 90 độ). Do đó, công thức tính diện tích hình thoi có thể áp dụng cho hình vuông, nhưng hình vuông cũng có công thức riêng đơn giản hơn là cạnh nhân cạnh (S = a²).

6. Khi nào công thức diện tích hình thoi qua cạnh và chiều cao được sử dụng?
Công thức diện tích hình thoi qua cạnh và chiều cao (S = a * h) thường được sử dụng khi bạn biết độ dài của một cạnh và chiều cao tương ứng của hình thoi, mà không biết độ dài của hai đường chéo. Đây là một công thức hữu ích trong các bài toán thực tế khi việc đo chiều cao dễ hơn đo đường chéo.

7. Có mẹo nào giúp học sinh dễ nhớ công thức tính diện tích hình thoi không?
Có. Một mẹo phổ biến là nhớ câu "Nửa tích hai đường chéo", tức là lấy độ dài đường chéo thứ nhất nhân với độ dài đường chéo thứ hai rồi chia cho 2. Việc hình dung hình thoi như một viên kim cương bị cắt làm đôi cũng giúp ghi nhớ công thức này.