Tâm Đối Xứng Là Gì? Định Nghĩa & Ví Dụ Chi Tiết Nhất

Bạn có bao giờ ngắm nhìn một bông hoa, một chiếc lá, hay một thiết kế kiến trúc và trầm trồ trước sự cân đối hoàn hảo của chúng? Đó chính là lúc khái niệm về sự đối xứng, đặc biệt là tâm đối xứng là gì, trở nên rõ nét. Tâm đối xứng không chỉ là một thuật ngữ trừu tượng trong hình học mà còn là nguyên lý cơ bản ẩn chứa vẻ đẹp và sự hài hòa trong thế giới tự nhiên và các công trình nhân tạo. Bài viết này sẽ đưa bạn khám phá sâu hơn về khái niệm thú vị này, từ định nghĩa cơ bản đến những ví dụ minh họa sinh động và ứng dụng của nó trong cuộc sống.

Tâm Đối Xứng Là Gì? Định Nghĩa Chi Tiết Nhất

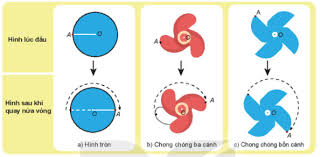
Trong hình học, khi nói đến tâm đối xứng là gì, chúng ta đang đề cập đến một điểm đặc biệt mà qua đó, một hình hoặc một đối tượng có thể "gấp" lại chính nó một cách hoàn hảo. Hiểu một cách đơn giản hơn, nếu bạn xoay một hình quanh một điểm cố định một góc 180 độ (nửa vòng), mà hình đó vẫn trùng khít với vị trí ban đầu của nó, thì điểm cố định đó chính là tâm đối xứng của hình.

"Tâm đối xứng là điểm mà nếu thực hiện phép quay 180 độ quanh điểm đó, hình sẽ trùng khít với chính nó. Đây là một khái niệm nền tảng, giúp chúng ta hiểu về sự cân bằng và cấu trúc của các hình khối."

— GS.TS. Nguyễn Văn A, Chuyên gia Hình học Phẳng

Cụ thể hơn:

• Định nghĩa hình có tâm đối xứng: Một hình H được gọi là có tâm đối xứng nếu tồn tại một điểm O sao cho khi thực hiện phép đối xứng tâm O (phép quay 180 độ quanh O), hình H biến thành chính nó. Điểm O đó được gọi là tâm đối xứng của hình H.
• Phép đối xứng tâm: Phép đối xứng tâm O là phép biến hình biến mỗi điểm M thành điểm M' sao cho O là trung điểm của đoạn thẳng MM'.

Điều này có nghĩa là, với bất kỳ điểm nào trên hình, nếu bạn vẽ một đường thẳng đi qua điểm đó và tâm đối xứng, bạn sẽ tìm thấy một điểm khác trên hình ở phía đối diện và cách đều tâm đối xứng. Đây là một thuộc tính độc đáo, tạo nên sự cân bằng và vẻ đẹp hài hòa cho các đối tượng có tâm đối xứng.

Các Đặc Điểm Quan Trọng Của Tâm Đối Xứng

Tâm đối xứng mang đến những đặc điểm nổi bật, giúp chúng ta nhận diện và hiểu rõ hơn về các hình có tính chất này:

• Tính duy nhất: Nếu một hình có tâm đối xứng, thì tâm đối xứng đó là duy nhất. Không có hai điểm khác nhau có thể cùng là tâm đối xứng của một hình.
• Tính trung điểm: Với bất kỳ cặp điểm A và A' nào đối xứng với nhau qua tâm O, thì O luôn là trung điểm của đoạn thẳng AA'.
• Bảo toàn khoảng cách và góc: Phép đối xứng tâm là một phép dời hình, tức là nó bảo toàn khoảng cách giữa hai điểm bất kỳ và độ lớn của các góc. Điều này có nghĩa là hình ban đầu và hình sau khi đối xứng sẽ có kích thước và hình dạng hoàn toàn giống nhau.
• Đường thẳng biến thành đường thẳng: Một đường thẳng đi qua tâm đối xứng sẽ biến thành chính nó khi thực hiện phép đối xứng tâm. Một đường thẳng không đi qua tâm đối xứng sẽ biến thành một đường thẳng song song với nó.
• Hình tròn có tâm là tâm đối xứng: Mọi hình tròn đều có tâm của nó là tâm đối xứng.

Các Hình Có Tâm Đối Xứng Phổ Biến Trong Hình Học

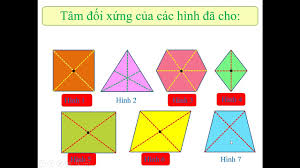
Bạn có thể dễ dàng tìm thấy các hình có tâm đối xứng trong đời sống và trong các bài toán hình học. Dưới đây là một số ví dụ điển hình về hình nào có tâm đối xứng và vị trí của chúng:

• Hình chữ nhật: Tâm đối xứng là giao điểm của hai đường chéo.
• Hình bình hành: Tương tự hình chữ nhật, tâm đối xứng là giao điểm của hai đường chéo.
• Hình thoi: Tâm đối xứng là giao điểm của hai đường chéo.
• Hình vuông: Là trường hợp đặc biệt của hình chữ nhật và hình thoi, tâm đối xứng cũng là giao điểm của hai đường chéo.
• Đường tròn: Tâm đối xứng chính là tâm của đường tròn đó.
• Hình lục giác đều: Tâm đối xứng là giao điểm của các đường chéo chính.
• Đoạn thẳng: Tâm đối xứng là trung điểm của đoạn thẳng đó.
• Điểm: Bản thân một điểm cũng có thể được coi là có tâm đối xứng chính là điểm đó.
• Đồ thị hàm số bậc ba: Một số hàm số bậc ba như y = ax^3 + bx^2 + cx + d có tâm đối xứng tại điểm uốn của đồ thị.

Phân Biệt Tâm Đối Xứng Và Trục Đối Xứng

Để hiểu rõ hơn về tâm đối xứng là gì, điều quan trọng là phân biệt nó với khái niệm "trục đối xứng". Cả hai đều nói về sự cân bằng nhưng theo những cách khác nhau:

Tiêu chí	Tâm Đối Xứng	Trục Đối Xứng
Bản chất	Một điểm mà qua đó hình quay 180 độ trùng khít.	Một đường thẳng mà qua đó hình "gấp" lại trùng khít.
Phép biến hình	Phép quay 180 độ (hay phép đối xứng tâm).	Phép lật qua đường thẳng (hay phép đối xứng trục).
Số lượng	Nếu có thì chỉ có 1 tâm đối xứng.	Một hình có thể có 0, 1, 2 hoặc nhiều trục đối xứng (ví dụ: hình tròn có vô số trục đối xứng).
Ví dụ	Hình chữ nhật, hình bình hành, đường tròn.	Hình thang cân, tam giác cân, hình tròn, hình vuông.

Cách Xác Định Tâm Đối Xứng Của Một Hình

Việc xác định tâm đối xứng của một hình thường phụ thuộc vào loại hình đó. Tuy nhiên, có một số nguyên tắc chung và cách tiếp cận cụ thể:

1. Đối với các hình đa giác đơn giản (hình chữ nhật, hình bình hành, hình thoi, hình vuông):
   • Vẽ hai đường chéo của hình.
   • Giao điểm của hai đường chéo đó chính là tâm đối xứng.
2. Đối với đường tròn:
   • Tâm của đường tròn chính là tâm đối xứng của nó.
3. Đối với đoạn thẳng:
   • Tâm đối xứng là trung điểm của đoạn thẳng đó.
4. Phương pháp tổng quát (dùng cho các hình phức tạp hơn):
   • Chọn một điểm A bất kỳ trên hình.
   • Tìm điểm A' là điểm đối xứng với A qua một điểm O giả định (nghĩa là O là trung điểm của AA').
   • Nếu điểm A' cũng nằm trên hình, và điều này đúng với mọi điểm A trên hình, thì O chính là tâm đối xứng. Cách này thường dùng trong các chứng minh toán học.
   • Nếu không biết O, có thể chọn hai điểm A, B trên hình, tìm trung điểm I của AB. Sau đó kiểm tra xem nếu hình đối xứng qua I có trùng khít không. Phương pháp này đòi hỏi sự kiểm tra kỹ lưỡng.

Hãy nhớ rằng không phải hình nào cũng có tâm đối xứng. Ví dụ, một tam giác đều có trục đối xứng nhưng không có tâm đối xứng.

Ứng Dụng Của Tâm Đối Xứng Trong Đời Sống & Khoa Học

Khái niệm tâm đối xứng là gì không chỉ dừng lại ở các bài toán hình học mà còn có nhiều ứng dụng thú vị trong thực tế:

• Kiến trúc và Thiết kế: Nhiều công trình kiến trúc nổi tiếng, logo thương hiệu, hay các tác phẩm nghệ thuật đều tận dụng tâm đối xứng để tạo ra sự cân bằng, hài hòa và thẩm mỹ. Ví dụ, một số đền thờ, nhà thờ, hoặc các mô hình mandala đều thể hiện rõ nét tính đối xứng tâm.
• Tự nhiên: Trong thế giới tự nhiên, tâm đối xứng xuất hiện ở nhiều dạng. Các bông hoa có hình dạng gần như tròn, một số loài sao biển, hay các tinh thể khoáng vật thường có cấu trúc đối xứng tâm, tạo nên vẻ đẹp kỳ diệu.
• Khoa học và Công nghệ: Trong hóa học, một số phân tử có tâm đối xứng. Trong vật lý, việc nghiên cứu các hệ thống có đối xứng tâm giúp đơn giản hóa các phương trình và mô hình. Trong công nghệ, các bộ phận máy móc, bánh răng, hay mạch điện tử cũng thường được thiết kế với tính đối xứng để đảm bảo hiệu suất và độ bền.
• Nghệ thuật và Đồ họa: Họa sĩ và nhà thiết kế đồ họa sử dụng tâm đối xứng để tạo ra các bố cục mạnh mẽ, thu hút ánh nhìn và truyền tải thông điệp một cách hiệu quả.

Sự hiện diện của tâm đối xứng trong nhiều lĩnh vực cho thấy tầm quan trọng của nó không chỉ về mặt lý thuyết mà còn trong việc tạo ra sự hài hòa và hiệu quả trong thế giới xung quanh chúng ta.

Kết Luận

Qua bài viết này, hy vọng bạn đã có cái nhìn toàn diện và sâu sắc hơn về tâm đối xứng là gì – một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học và cuộc sống. Từ định nghĩa, các đặc điểm, đến những ví dụ cụ thể và ứng dụng thực tiễn, tâm đối xứng không chỉ là một phép toán mà còn là một nguyên lý thẩm mỹ, tạo nên sự cân bằng và vẻ đẹp trong nhiều khía cạnh của thế giới chúng ta. Việc nắm vững khái niệm này không chỉ giúp bạn giải quyết tốt các bài tập hình học mà còn mở ra một góc nhìn mới về sự hài hòa và cấu trúc tự nhiên.

Hãy thử tìm kiếm các vật thể có tâm đối xứng xung quanh bạn và khám phá vẻ đẹp tiềm ẩn của chúng!

Câu Hỏi Thường Gặp (FAQ) Về Tâm Đối Xứng

1. Tâm đối xứng là gì trong toán học?

Trong toán học, tâm đối xứng là một điểm mà qua đó nếu ta quay một hình 180 độ, hình đó sẽ trùng khít với vị trí ban đầu. Đây là một khái niệm cơ bản của phép đối xứng tâm trong hình học.

2. Những hình nào thường có tâm đối xứng?

Các hình phổ biến có tâm đối xứng bao gồm hình chữ nhật, hình bình hành, hình thoi, hình vuông, đường tròn, đoạn thẳng, và hình lục giác đều. Giao điểm của các đường chéo thường là tâm đối xứng.

3. Làm thế nào để xác định tâm đối xứng của một hình chữ nhật?

Để xác định tâm đối xứng của một hình chữ nhật, bạn chỉ cần vẽ hai đường chéo của hình đó. Giao điểm của hai đường chéo chính là tâm đối xứng của hình chữ nhật.

4. Có phải mọi hình đều có tâm đối xứng không?

Không, không phải mọi hình đều có tâm đối xứng. Ví dụ, một tam giác (trừ trường hợp suy biến) hoặc một hình thang cân thường không có tâm đối xứng, mặc dù chúng có thể có trục đối xứng.

5. Phân biệt tâm đối xứng và trục đối xứng như thế nào?

Tâm đối xứng là một điểm mà hình quay 180 độ trùng khít, trong khi trục đối xứng là một đường thẳng mà hình có thể gấp lại trùng khít. Tâm đối xứng liên quan đến phép quay, trục đối xứng liên quan đến phép lật.

6. Ứng dụng của tâm đối xứng trong đời sống là gì?

Tâm đối xứng có nhiều ứng dụng trong thiết kế kiến trúc, nghệ thuật, logo thương hiệu, và cả trong tự nhiên (như cấu trúc của hoa, tinh thể). Nó tạo ra sự cân bằng, hài hòa và tính thẩm mỹ cho các đối tượng.