Tam Giác Vuông: Khám Phá Toàn Diện Về Hình Học Cơ Bản và Ứng Dụng

Trong thế giới hình học phẳng, có lẽ không một hình nào lại quen thuộc và mang tính ứng dụng cao như tam giác vuông. Từ những công trình kiến trúc đồ sộ đến các phép đo đạc địa lý phức tạp, sự hiện diện của nó là không thể phủ nhận. Vậy, đâu là điều làm nên sự đặc biệt của tam giác vuông? Bài viết này sẽ đưa bạn đi sâu vào định nghĩa, các tính chất quan trọng, công thức tính toán và những ứng dụng thú vị của nó trong đời sống, giúp bạn có cái nhìn toàn diện nhất.

Định Nghĩa Tam Giác Vuông: Nền Tảng Của Hình Học

Một cách đơn giản nhất, tam giác vuông là một loại tam giác đặc biệt, được xác định bởi sự hiện diện của một góc có số đo đúng bằng 90 độ (hay còn gọi là góc vuông).

Khái Niệm Cơ Bản

Mọi tam giác đều có ba cạnh và ba góc. Tuy nhiên, để được gọi là tam giác vuông, một trong ba góc đó phải là góc vuông. Hai góc còn lại sẽ là góc nhọn (nhỏ hơn 90 độ) và tổng của chúng luôn bằng 90 độ, bởi tổng ba góc trong một tam giác luôn là 180 độ.

Các Thành Phần Quan Trọng Của Một Tam Giác Vuông

Để hiểu rõ hơn về tam giác vuông, chúng ta cần nắm vững các thuật ngữ sau:

• Góc vuông: Chính là góc 90 độ, là đặc điểm nhận dạng của tam giác vuông.
• Cạnh góc vuông (cạnh kề): Là hai cạnh tạo nên góc vuông. Chúng còn được gọi là cạnh góc vuông hoặc cạnh kề của góc vuông.
• Cạnh huyền: Là cạnh đối diện với góc vuông và cũng là cạnh dài nhất trong tam giác vuông.

Hãy hình dung một chiếc thang dựa vào tường. Tường và sàn nhà tạo thành một góc vuông, và chiếc thang chính là cạnh huyền, còn tường và sàn là hai cạnh góc vuông. Sự đơn giản trong cấu trúc này lại mở ra vô vàn những tính chất và định lý thú vị.

Các Định Lý Quan Trọng Liên Quan Đến Tam Giác Vuông

Sức mạnh của tam giác vuông không chỉ nằm ở định nghĩa mà còn ở những định lý toán học sâu sắc được xây dựng dựa trên nó.

Định Lý Pytago: Viên Đá Đầu Tiên

Khi nhắc đến tam giác vuông, không thể không nhắc đến Định lý Pytago – một trong những định lý nổi tiếng và quan trọng nhất của toán học cổ đại, được đặt theo tên của nhà toán học Hy Lạp Pythagoras. Định lý này thiết lập mối quan hệ giữa độ dài các cạnh của một tam giác vuông.

Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.

Nếu gọi độ dài hai cạnh góc vuông là 'a' và 'b', và độ dài cạnh huyền là 'c', công thức của Định lý Pytago sẽ là:

a2 + b2 = c2

Ví dụ minh họa:

Giả sử bạn có một tam giác vuông với hai cạnh góc vuông lần lượt là 3 cm và 4 cm. Áp dụng định lý Pytago, ta có:

• 32 + 42 = c2
• 9 + 16 = c2
• 25 = c2
• c = √25 = 5 cm

Vậy, cạnh huyền của tam giác vuông này là 5 cm. Định lý này là chìa khóa để giải quyết rất nhiều bài toán liên quan đến độ dài trong không gian.

Định Lý Thuận và Đảo của Pytago

Định lý Pytago không chỉ có chiều thuận mà còn có chiều đảo, giúp chúng ta xác định một tam giác có phải là tam giác vuông hay không:

Định lý Pytago thuận: Nếu một tam giác là tam giác vuông thì bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Định lý Pytago đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại, thì tam giác đó là tam giác vuông (cạnh có bình phương lớn nhất chính là cạnh huyền).

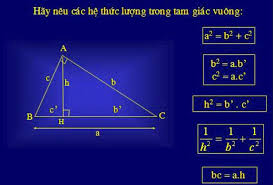
Hệ Thức Lượng Trong Tam Giác Vuông

Ngoài định lý Pytago, trong tam giác vuông còn có các hệ thức lượng quan trọng khác liên quan đến đường cao kẻ từ đỉnh góc vuông xuống cạnh huyền, và hình chiếu của các cạnh góc vuông trên cạnh huyền. Các hệ thức này giúp chúng ta tính toán nhiều yếu tố khác của tam giác vuông khi biết một số thông tin nhất định.

Công Thức Tính Toán Phổ Biến

Việc tính toán các đại lượng cơ bản như diện tích và chu vi của tam giác vuông là vô cùng cần thiết trong nhiều lĩnh vực.

Cách Tính Diện Tích Tam Giác Vuông

Diện tích của bất kỳ tam giác nào cũng được tính bằng công thức: (1/2) * đáy * chiều cao. Đối với tam giác vuông, hai cạnh góc vuông đóng vai trò là đáy và chiều cao, vì chúng vuông góc với nhau.

Công thức tính diện tích S của tam giác vuông với hai cạnh góc vuông là 'a' và 'b':

S = (1/2) * a * b

Ví dụ: Tam giác vuông có cạnh góc vuông 6cm và 8cm. Diện tích là: S = (1/2) * 6 * 8 = 24 cm2.

Cách Tính Chu Vi Tam Giác Vuông

Chu vi của một tam giác là tổng độ dài của ba cạnh của nó. Đối với tam giác vuông, nếu biết độ dài hai cạnh góc vuông (a, b) và cạnh huyền (c), chu vi P sẽ là:

P = a + b + c

Nếu chỉ biết hai cạnh góc vuông, bạn có thể dùng Định lý Pytago để tìm cạnh huyền trước, sau đó tính chu vi.

Một Số Dạng Tam Giác Vuông Đặc Biệt

Bên cạnh tam giác vuông tổng quát, có một số trường hợp đặc biệt thường gặp trong toán học và các bài toán thực tế.

Tam Giác Vuông Cân

Tam giác vuông cân là một loại tam giác vuông mà hai cạnh góc vuông của nó có độ dài bằng nhau. Điều này đồng nghĩa với việc hai góc nhọn của nó cũng bằng nhau và mỗi góc có số đo là 45 độ. Tam giác vuông cân là một hình đối xứng và thường xuất hiện trong các bài toán hình học cơ bản.

Tam Giác Vuông Với Các Góc 30-60-90 Độ

Đây là một dạng tam giác vuông đặc biệt khác, có các góc lần lượt là 30 độ, 60 độ và 90 độ. Mối quan hệ giữa các cạnh của nó cũng rất đặc biệt: cạnh đối diện với góc 30 độ bằng một nửa cạnh huyền, và cạnh đối diện với góc 60 độ bằng cạnh đối diện với góc 30 độ nhân với √3.

Ứng Dụng Thực Tiễn Của Tam Giác Vuông Trong Đời Sống

Có thể bạn không nhận ra, nhưng tam giác vuông hiện diện ở khắp mọi nơi xung quanh chúng ta, từ những vật dụng đơn giản đến các công trình phức tạp.

Kiến trúc và Xây dựng

Trong kiến trúc và xây dựng, tam giác vuông là công cụ không thể thiếu. Các kiến trúc sư và kỹ sư sử dụng nó để đảm bảo độ vuông góc của các bức tường, sàn nhà, mái nhà. Định lý Pytago giúp tính toán chiều dài các thanh chống, dầm, và đảm bảo sự vững chắc cho cấu trúc.

"Mỗi viên gạch được đặt vuông vắn, mỗi góc nhà thẳng hàng đều chứa đựng nguyên lý của tam giác vuông. Nó là nền tảng cho sự ổn định và cân bằng của mọi công trình." - Một kỹ sư xây dựng giả định.

Điều hướng và Bản đồ

Các nhà hàng hải và địa chất sử dụng tam giác vuông để xác định vị trí, khoảng cách và góc. Ví dụ, việc xác định vị trí của một con tàu trên biển hoặc độ cao của một ngọn núi thường dựa trên nguyên tắc tam giác vuông và lượng giác.

Khoa học và Công nghệ

Trong vật lý, việc phân tích các vector lực thường sử dụng tam giác vuông. Trong đồ họa máy tính, tam giác vuông là khối xây dựng cơ bản để tạo ra các hình dạng 3D. Ngay cả trong thiết kế đồ họa và nghệ thuật, nguyên tắc tỷ lệ vàng và các hình khối đối xứng thường có nguồn gốc từ các tính chất của tam giác vuông.

Làm Thế Nào Để Chứng Minh Một Tam Giác Là Tam Giác Vuông?

Có một số cách phổ biến để chứng minh một tam giác là tam giác vuông:

1. Dùng Định lý Pytago đảo: Nếu bình phương một cạnh bằng tổng bình phương hai cạnh kia. Đây là cách phổ biến nhất và hiệu quả nhất.
2. Dùng tổng ba góc: Nếu một trong ba góc của tam giác có số đo là 90 độ.
3. Dùng tính chất đường trung tuyến: Nếu đường trung tuyến ứng với một cạnh của tam giác bằng một nửa cạnh đó, thì tam giác đó là tam giác vuông (cạnh đó chính là cạnh huyền).

Kết Luận

Từ định nghĩa đơn giản đến những định lý phức tạp và ứng dụng rộng rãi, tam giác vuông thực sự là một khái niệm trung tâm trong hình học và toán học nói chung. Nó không chỉ là một công cụ lý thuyết mà còn là chìa khóa để giải quyết vô số vấn đề trong thế giới thực. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn sâu sắc và toàn diện về tầm quan trọng của tam giác vuông. Hãy tiếp tục khám phá và ứng dụng những kiến thức này vào học tập và cuộc sống!

Câu Hỏi Thường Gặp Về Tam Giác Vuông (FAQ)

Tam giác vuông là gì?

Tam giác vuông là một loại tam giác có một góc đo bằng 90 độ. Đây là đặc điểm nhận dạng cơ bản và quan trọng nhất của nó trong hình học.

Tại sao Định lý Pytago lại quan trọng đối với tam giác vuông?

Định lý Pytago thiết lập mối quan hệ toán học giữa độ dài ba cạnh của một tam giác vuông (a² + b² = c²). Nó cực kỳ quan trọng vì giúp tính toán độ dài các cạnh khi biết hai cạnh còn lại, ứng dụng rộng rãi trong xây dựng, kiến trúc và nhiều lĩnh vực khác.

Làm thế nào để tính diện tích của một tam giác vuông?

Để tính diện tích S của một tam giác vuông, bạn sử dụng công thức: S = (1/2) * cạnh góc vuông 1 * cạnh góc vuông 2. Hai cạnh góc vuông chính là đáy và chiều cao của tam giác.

Cạnh huyền của tam giác vuông là gì?

Cạnh huyền là cạnh dài nhất trong tam giác vuông, và nó luôn là cạnh đối diện với góc vuông (góc 90 độ). Đây là một khái niệm cơ bản khi nghiên cứu về tam giác vuông.

Có nên học kỹ về tam giác vuông không?

Tuyệt đối nên! Kiến thức về tam giác vuông là nền tảng cho nhiều lĩnh vực toán học cao hơn như lượng giác và hình học không gian, cũng như có vô số ứng dụng thực tế trong kỹ thuật, vật lý và đời sống.

Tam giác vuông có mấy góc nhọn?

Một tam giác vuông luôn có hai góc nhọn. Tổng số đo của hai góc nhọn này luôn bằng 90 độ, vì tổng ba góc trong một tam giác là 180 độ và một góc đã là 90 độ.

Ứng dụng của tam giác vuông trong đời sống là gì?

Tam giác vuông được ứng dụng rộng rãi trong kiến trúc (đảm bảo vuông góc, tính toán kết cấu), xây dựng, điều hướng (xác định vị trí), thiết kế đồ họa, và nhiều ngành khoa học kỹ thuật khác để giải quyết các bài toán về khoảng cách và góc.