Tia Phân Giác Là Gì? Giải Mã Khái Niệm, Tính Chất Và Ứng Dụng Trong Hình Học

Bạn đã bao giờ nghe đến cụm từ "tia phân giác" trong các bài học hình học chưa? Đây không chỉ là một khái niệm cơ bản mà còn là một công cụ cực kỳ quan trọng, mở ra cánh cửa hiểu biết sâu sắc về cấu trúc và mối quan hệ giữa các hình khối. Tia phân giác là gì và nó có vai trò như thế nào trong toán học cũng như đời sống? Hãy cùng chúng tôi khám phá chi tiết trong bài viết này, từ định nghĩa chuẩn xác đến các tính chất đặc trưng và ứng dụng thực tiễn không ngờ!

Tia Phân Giác Là Gì? Định Nghĩa Chuẩn Xác Nhất

Trong hình học phẳng, khi chúng ta nói đến một góc, đó là hình tạo bởi hai tia chung gốc. Và rồi, tia phân giác là gì? Đơn giản, nó chính là "người chia đôi" hoàn hảo. Một tia phân giác của một góc là tia nằm giữa hai cạnh của góc đó và tạo với mỗi cạnh của góc hai góc bằng nhau.

Định nghĩa: Tia phân giác của một góc là tia xuất phát từ đỉnh của góc, đi qua miền trong của góc và chia góc đó thành hai góc nhỏ có số đo bằng nhau.

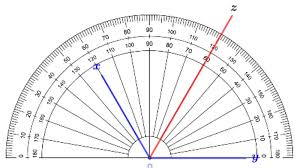
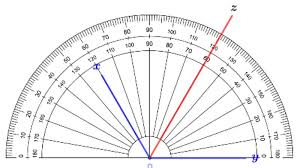
Ví dụ, nếu chúng ta có góc xOy, và tia Oz là tia phân giác của góc xOy, thì điều đó có nghĩa là tia Oz nằm giữa hai tia Ox và Oy, đồng thời góc xOz sẽ bằng góc zOy.

Điều này không chỉ giúp chúng ta xác định một cách chính xác vị trí của một tia so với một góc mà còn là nền tảng cho nhiều định lý và tính chất quan trọng khác trong hình học. Nắm vững khái niệm cơ bản này là bước đầu tiên để bạn có thể giải quyết các bài toán phức tạp hơn.

Các Tính Chất Nổi Bật Của Tia Phân Giác

Không chỉ dừng lại ở định nghĩa, tia phân giác còn sở hữu những tính chất vô cùng đặc biệt, là chìa khóa để giải quyết nhiều bài toán hình học. Vậy những tính chất cơ bản của tia phân giác là gì?

Tính chất 1: Điểm nằm trên tia phân giác cách đều hai cạnh của góc

Đây là một trong những tính chất quan trọng nhất và thường được sử dụng để chứng minh trong các bài toán. Nếu một điểm bất kỳ nằm trên tia phân giác của một góc, thì khoảng cách từ điểm đó đến hai cạnh của góc là bằng nhau.

• Giả sử tia Oz là tia phân giác của góc xOy.
• Lấy điểm M bất kỳ trên tia Oz.
• Kẻ MH vuông góc với Ox tại H và MK vuông góc với Oy tại K.
• Khi đó, ta luôn có MH = MK.

Tính chất này là cơ sở để tìm một điểm có tính chất đối xứng hoặc xác định vị trí tối ưu trong nhiều bài toán thực tế, chẳng hạn như tìm vị trí một nguồn nước cách đều hai con đường.

Tính chất 2: Tập hợp các điểm cách đều hai cạnh của góc là tia phân giác

Đây là một dạng đảo của tính chất thứ nhất. Nếu một điểm nằm trong miền của một góc và cách đều hai cạnh của góc đó, thì điểm đó phải nằm trên tia phân giác của góc.

Mối quan hệ hai chiều: Một điểm nằm trên tia phân giác khi và chỉ khi điểm đó cách đều hai cạnh của góc.

Sự tương đương này cho phép chúng ta không chỉ xác định một điểm nằm trên tia phân giác mà còn có thể chứng minh một tia là tia phân giác dựa trên tính chất khoảng cách.

Tia Phân Giác Của Góc Bẹt Là Gì?

Góc bẹt là một góc có số đo bằng 180 độ. Tia phân giác của góc bẹt có một tính chất đặc biệt. Đó chính là đường thẳng vuông góc với đường thẳng chứa góc bẹt tại đỉnh của góc đó. Nói cách khác, nó chia góc bẹt thành hai góc vuông (90 độ).

Hướng Dẫn Cách Vẽ Tia Phân Giác Đơn Giản, Chính Xác

Sau khi đã hiểu rõ tia phân giác là gì và các tính chất của nó, việc thực hành cách vẽ là bước tiếp theo để củng cố kiến thức. Có hai cách phổ biến để vẽ tia phân giác của một góc: sử dụng thước thẳng và compa, hoặc sử dụng thước đo góc.

Cách Vẽ Bằng Thước Thẳng Và Compa

Đây là phương pháp cơ bản và chính xác, thường được dùng trong các bài toán hình học yêu cầu độ chính xác cao:

1. Bước 1: Đặt đầu nhọn của compa vào đỉnh O của góc xOy.
2. Bước 2: Vẽ một cung tròn cắt hai cạnh Ox và Oy của góc tại hai điểm A và B (điều chỉnh độ mở compa sao cho phù hợp).
3. Bước 3: Giữ nguyên độ mở của compa (hoặc thay đổi tùy ý nhưng phải giữ nguyên cho bước này và bước tiếp theo). Đặt đầu nhọn của compa vào điểm A và vẽ một cung tròn trong lòng góc.
4. Bước 4: Tương tự, đặt đầu nhọn của compa vào điểm B và vẽ một cung tròn khác cắt cung tròn vừa vẽ ở bước 3 tại một điểm M.
5. Bước 5: Dùng thước thẳng kẻ một tia từ đỉnh O đi qua điểm M. Tia Om chính là tia phân giác của góc xOy.

Phương pháp này đảm bảo tính đối xứng và độ chính xác hình học, không phụ thuộc vào việc đọc số đo góc.

Cách Vẽ Bằng Thước Đo Góc

Đây là phương pháp nhanh gọn, phù hợp khi bạn cần xác định tia phân giác một cách nhanh chóng hoặc khi góc có số đo cụ thể:

1. Bước 1: Đặt tâm của thước đo góc trùng với đỉnh O của góc xOy, sao cho một cạnh của góc (ví dụ Ox) trùng với vạch 0 độ của thước.
2. Bước 2: Đọc số đo của góc xOy (ví dụ là N độ) trên thước.
3. Bước 3: Chia số đo góc vừa đọc cho 2 (N/2).
4. Bước 4: Đánh dấu một điểm trên thước tại vị trí N/2 độ.
5. Bước 5: Dùng thước thẳng kẻ một tia từ đỉnh O đi qua điểm vừa đánh dấu. Tia này chính là tia phân giác của góc xOy.

Mặc dù nhanh, phương pháp này có thể có sai số nhỏ tùy thuộc vào độ chính xác của thước và mắt người đọc.

Tia Phân Giác Trong Tam Giác: Khái Niệm Và Ứng Dụng

Khi áp dụng vào tam giác, khái niệm tia phân giác trở nên phong phú hơn với những tính chất đặc biệt và ứng dụng sâu rộng. Vậy vai trò của tia phân giác trong tam giác là gì?

Định Nghĩa Đường Phân Giác Trong Tam Giác

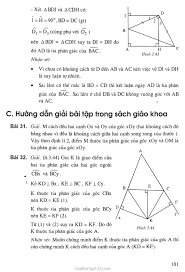
Trong một tam giác, đường phân giác của một góc là đoạn thẳng nối đỉnh của góc đó với một điểm trên cạnh đối diện, sao cho đoạn thẳng này là một phần của tia phân giác của góc.

• Mỗi tam giác có ba đường phân giác, mỗi đường xuất phát từ một đỉnh.
• Ví dụ: Trong tam giác ABC, đường phân giác xuất phát từ đỉnh A là đoạn thẳng AD, với D nằm trên cạnh BC và tia AD là tia phân giác của góc BAC.

Tính Chất Ba Đường Phân Giác Trong Tam Giác

Một trong những tính chất đẹp nhất của ba đường phân giác trong tam giác là chúng luôn đồng quy tại một điểm duy nhất. Điểm đồng quy này được gọi là tâm đường tròn nội tiếp của tam giác.

• Điểm này cách đều ba cạnh của tam giác.
• Từ điểm này, chúng ta có thể vẽ một đường tròn tiếp xúc với cả ba cạnh của tam giác (đường tròn nội tiếp).

Tính chất này có ý nghĩa quan trọng trong việc giải các bài toán về đường tròn, khoảng cách và các mối quan hệ hình học phức tạp khác.

Ứng Dụng Của Tia Phân Giác Trong Tam Giác

Đường phân giác không chỉ là một lý thuyết suông. Nó có nhiều ứng dụng thực tế:

• Trong thiết kế kiến trúc: Giúp xác định các đường đối xứng, tối ưu hóa không gian hoặc vị trí đặt các yếu tố trang trí.
• Trong quang học: Tia phân giác có thể giúp mô tả đường đi của ánh sáng khi phản xạ hoặc khúc xạ qua các bề mặt đối xứng.
• Trong kỹ thuật: Giúp tạo ra các chi tiết máy móc có độ cân bằng và đối xứng cao.
• Trong các bài toán tối ưu hóa: Ví dụ, tìm điểm có khoảng cách tối thiểu đến các đối tượng khác.

Ứng Dụng Thực Tế Của Tia Phân Giác

Ngoài những ứng dụng trong hình học và tam giác, liệu bạn có bao giờ tự hỏi: vai trò của tia phân giác là gì trong cuộc sống hàng ngày?

"Khái niệm tia phân giác không chỉ là một công cụ lý thuyết mà còn là nền tảng cho nhiều ứng dụng thực tiễn trong các lĩnh vực từ thiết kế, kiến trúc đến công nghệ."

Mặc dù chúng ta không nhìn thấy tia phân giác một cách trực tiếp, nhưng nguyên lý của nó lại hiện diện khắp nơi:

• Kiến trúc và Xây dựng: Khi thiết kế một căn phòng hoặc một cây cầu, các kỹ sư và kiến trúc sư thường sử dụng các nguyên tắc đối xứng và cân bằng. Tia phân giác giúp họ xác định các trục đối xứng, đảm bảo sự ổn định và hài hòa cho công trình. Ví dụ, vị trí của một đèn chùm trong một căn phòng vuông thường được đặt tại giao điểm của các đường phân giác của các góc tường để ánh sáng được phân bổ đều.
• Nghệ thuật và Thiết kế: Trong hội họa, điêu khắc, hay thiết kế đồ họa, việc tạo ra sự cân đối và điểm nhấn thường dựa trên các đường đối xứng và phân chia không gian. Tia phân giác cung cấp một phương pháp tự nhiên để chia một góc hoặc một khu vực thành các phần bằng nhau, tạo ra sự hài hòa thị giác.
• Quang học và Vật lý: Trong các thiết bị quang học như kính thiên văn, kính hiển vi hoặc máy ảnh, nguyên tắc tia phân giác có thể liên quan đến đường đi của ánh sáng qua các thấu kính để tạo ra hình ảnh sắc nét và cân đối. Tia sáng tới và tia sáng phản xạ từ một mặt phẳng gương sẽ tạo ra một góc mà đường pháp tuyến (đường vuông góc với gương tại điểm tới) chính là tia phân giác của góc tạo bởi tia tới và tia phản xạ.
• Địa lý và Bản đồ: Khi xác định vị trí tối ưu của một trạm phát sóng hoặc một điểm phục vụ cộng đồng sao cho nó cách đều các khu dân cư khác nhau, nguyên lý của tia phân giác có thể được áp dụng để tìm điểm cách đều các đường hoặc các khu vực.
• Robot học: Trong lập trình robot di chuyển trong một không gian hạn chế, việc xác định các "đường trung bình" hoặc "đường tránh vật cản" cách đều hai vật cản song song có thể liên quan đến khái niệm tia phân giác.

Rõ ràng, hiểu được tia phân giác là gì không chỉ giúp bạn giỏi toán hơn mà còn mở ra một cái nhìn mới về cách thế giới xung quanh chúng ta được thiết kế và vận hành theo những nguyên tắc hình học cơ bản.

Kết Luận

Qua bài viết này, chúng ta đã cùng nhau khám phá sâu hơn về khái niệm "tia phân giác là gì", từ định nghĩa cơ bản đến những tính chất quan trọng và cách vẽ chi tiết. Tia phân giác không chỉ là một khái niệm trừu tượng trong sách giáo khoa mà còn là một công cụ mạnh mẽ với nhiều ứng dụng thực tế trong đa dạng lĩnh vực. Nắm vững kiến thức về tia phân giác sẽ giúp bạn không chỉ giải quyết các bài toán hình học một cách dễ dàng hơn mà còn phát triển tư duy logic và khả năng quan sát thế giới dưới góc nhìn toán học. Hãy tiếp tục thực hành và áp dụng những kiến thức này để mở rộng hiểu biết của mình nhé!

FAQ - Các Câu Hỏi Thường Gặp Về Tia Phân Giác

1. Tia phân giác là gì trong hình học cơ bản?

   Tia phân giác là một tia xuất phát từ đỉnh của một góc, nằm trong lòng góc đó và chia góc thành hai góc nhỏ có số đo bằng nhau. Đây là một khái niệm nền tảng trong hình học phẳng.

2. Tính chất quan trọng nhất của tia phân giác là gì?

   Tính chất quan trọng nhất là mọi điểm nằm trên tia phân giác của một góc đều cách đều hai cạnh của góc đó. Điều này tạo nên sự đối xứng và là cơ sở cho nhiều ứng dụng.

3. Làm thế nào để vẽ tia phân giác của một góc bằng compa?

   Để vẽ tia phân giác, bạn dùng compa vẽ hai cung tròn từ đỉnh góc cắt hai cạnh, sau đó dùng cùng bán kính vẽ hai cung tròn từ hai giao điểm này, điểm giao của hai cung đó sẽ nằm trên tia phân giác.

4. Tia phân giác có ứng dụng gì trong thực tế?

   Tia phân giác có nhiều ứng dụng thực tế như trong kiến trúc để tạo sự đối xứng, trong quang học để mô tả đường đi của ánh sáng, hoặc trong kỹ thuật để thiết kế các bộ phận cân bằng.

5. Giao điểm của ba đường phân giác trong tam giác là gì?

   Giao điểm của ba đường phân giác trong một tam giác được gọi là tâm đường tròn nội tiếp của tam giác. Điểm này cách đều ba cạnh của tam giác và là tâm của đường tròn tiếp xúc với cả ba cạnh.

6. Khi nào một tia được coi là tia phân giác?

   Một tia được coi là tia phân giác khi nó xuất phát từ đỉnh của góc, nằm giữa hai cạnh và chia góc đó thành hai phần bằng nhau. Hoặc, khi mọi điểm trên tia đó cách đều hai cạnh của góc.