Home
Sản Phẩm
Sản Phẩm 1 Sản Phẩm 2 Sản Phẩm 3
Phụ Kiện Khuyến Mãi
Home Sản Phẩm bài viết

Ước Chung Lớn Nhất: Khái Niệm, Cách Tính Và Ứng Dụng Đa Dạng

Ước Chung Lớn Nhất: Khái Niệm, Cách Tính Và Ứng Dụng Đa Dạng
Gallery 1 Gallery 2

In Stock



Total: $24.99 $9000

Add to Cart

Chính Sách Vận Chuyển Và Đổi Trả Hàng

Miễn phí vận chuyển mọi đơn hàng từ 500K

- Phí ship mặc trong nước 50K

- Thời gian nhận hàng 2-3 ngày trong tuần

- Giao hàng hỏa tốc trong 24h

- Hoàn trả hàng trong 30 ngày nếu không hài lòng

Mô tả sản phẩm

Ước Chung Lớn Nhất: Khái Niệm, Cách Tính Và Ứng Dụng Đa Dạng

Trong thế giới của toán học, có những khái niệm cơ bản nhưng lại đóng vai trò cực kỳ quan trọng, và ước chung lớn nhất (UCLN) chắc chắn là một trong số đó. Khái niệm này không chỉ là nền tảng cho nhiều bài toán số học phức tạp hơn mà còn có những ứng dụng bất ngờ trong cả đời sống hàng ngày. Bài viết này sẽ giúp bạn hiểu rõ UCLN là gì, các phương pháp tìm UCLN hiệu quả và cách nó được áp dụng vào thực tiễn.

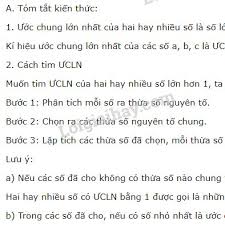
Định Nghĩa Ước Chung Lớn Nhất (UCLN) Là Gì?

Để hiểu về ước chung lớn nhất, trước tiên chúng ta cần làm rõ khái niệm "ước số chung". Một ước số chung của hai hay nhiều số tự nhiên là một số tự nhiên mà tất cả các số đó đều chia hết cho nó.

Ví dụ: Các ước của 12 là {1, 2, 3, 4, 6, 12}. Các ước của 18 là {1, 2, 3, 6, 9, 18}.

Từ đó, ta có thể thấy các ước chung của 12 và 18 là {1, 2, 3, 6}.

Và ước chung lớn nhất của hai hay nhiều số tự nhiên là số lớn nhất trong tập hợp các ước chung của chúng. Ký hiệu UCLN(a, b) hoặc ƯCLN(a, b).

Tiếp tục ví dụ trên, UCLN(12, 18) = 6.

"Hiểu được UCLN không chỉ giúp chúng ta giải quyết các bài toán toán học mà còn rèn luyện tư duy logic, phân tích vấn đề một cách có hệ thống. Nó là một viên gạch vững chắc trong nền móng kiến thức số học."

– Giáo sư Nguyễn Văn An, Chuyên gia Toán học

Các Phương Pháp Tìm Ước Chung Lớn Nhất Hiệu Quả

Có nhiều cách để tìm ước chung lớn nhất, từ những phương pháp đơn giản cho số nhỏ đến các thuật toán phức tạp hơn cho số lớn. Dưới đây là ba phương pháp phổ biến và hiệu quả nhất:

1. Phương Pháp Liệt Kê Ước Số

Đây là phương pháp cơ bản nhất, thường được dạy ở cấp tiểu học hoặc đầu cấp trung học cơ sở.

Cách thực hiện:

  1. Liệt kê tất cả các ước của từng số.
  2. Tìm các ước số chung giữa các tập hợp ước đã liệt kê.
  3. Chọn ước số lớn nhất trong số các ước chung đó.

Ví dụ: Tìm UCLN(20, 30)

  • Ước của 20: {1, 2, 4, 5, 10, 20}
  • Ước của 30: {1, 2, 3, 5, 6, 10, 15, 30}
  • Ước chung của 20 và 30: {1, 2, 5, 10}
  • Ước chung lớn nhất (UCLN) của 20 và 30 là 10.

Phương pháp này đơn giản nhưng có thể tốn thời gian khi làm việc với các số lớn.

2. Phương Pháp Phân Tích Thừa Số Nguyên Tố

Đây là phương pháp phổ biến và hiệu quả hơn, đặc biệt khi số cần tìm UCLN lớn.

Cách thực hiện:

  1. Phân tích mỗi số ra thừa số nguyên tố.
  2. Chọn các thừa số nguyên tố chung của tất cả các số.
  3. Với mỗi thừa số nguyên tố chung, chọn số mũ nhỏ nhất của nó.
  4. Nhân các thừa số nguyên tố đã chọn (với số mũ tương ứng) lại với nhau. Kết quả là UCLN.

Ví dụ: Tìm UCLN(72, 108)

  • Phân tích 72: 72 = 23 × 32
  • Phân tích 108: 108 = 22 × 33
  • Thừa số nguyên tố chung: 2 và 3.
  • Số mũ nhỏ nhất của 2 là 2 (từ 22).
  • Số mũ nhỏ nhất của 3 là 2 (từ 32).
  • UCLN(72, 108) = 22 × 32 = 4 × 9 = 36.

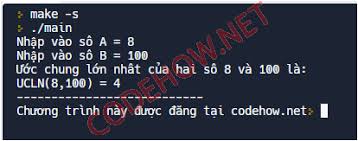
3. Thuật Toán Euclid (Thuật Toán Chia Liên Tiếp)

Đây là phương pháp hiệu quả nhất để tìm UCLN của hai số, đặc biệt là với các số rất lớn, vì nó không yêu cầu phân tích thừa số nguyên tố.

Cách thực hiện:

  1. Lấy số lớn chia cho số bé, lấy số dư.
  2. Nếu số dư bằng 0, thì số chia chính là UCLN.
  3. Nếu số dư khác 0, thay thế số lớn bằng số bé, số bé bằng số dư, và lặp lại bước 1.

Ví dụ: Tìm UCLN(252, 198)

  • 252 : 198 = 1 dư 54
  • 198 : 54 = 3 dư 36
  • 54 : 36 = 1 dư 18
  • 36 : 18 = 2 dư 0

Vì số dư cuối cùng bằng 0, số chia cuối cùng (18) chính là UCLN. Vậy, UCLN(252, 198) = 18.

Ứng Dụng Của Ước Chung Lớn Nhất Trong Đời Sống và Toán Học

UCLN không chỉ là một khái niệm trừu tượng mà còn có nhiều ứng dụng thực tiễn:

  • Rút gọn phân số: Đây là ứng dụng phổ biến nhất. Để rút gọn một phân số đến dạng tối giản, ta chia cả tử số và mẫu số cho UCLN của chúng.
    Ví dụ: Rút gọn phân số 48/60.
    UCLN(48, 60) = 12.
    Vậy 48/60 = (48 ÷ 12) / (60 ÷ 12) = 4/5.
  • Bài toán chia đều: Trong các bài toán chia nhóm, chia phần quà sao cho số lượng mỗi phần là lớn nhất và không còn dư, UCLN thường được sử dụng.
    Ví dụ: Có 24 viên kẹo và 36 cái bánh. Muốn chia thành các phần quà giống nhau, mỗi phần có số lượng kẹo và bánh nhiều nhất có thể. UCLN(24, 36) = 12. Vậy có thể chia thành 12 phần quà, mỗi phần có 2 viên kẹo và 3 cái bánh.
  • Thiết kế và kiến trúc: Trong một số trường hợp, UCLN có thể giúp xác định kích thước lớn nhất của các đơn vị vật liệu để lát sàn, xếp gạch mà không cần cắt ghép.
  • Trong lập trình máy tính: Thuật toán Euclid là một trong những thuật toán cơ bản và hiệu quả được sử dụng trong lập trình để tìm UCLN, phục vụ cho các phép toán liên quan đến số học.

Mối Quan Hệ Giữa Ước Chung Lớn Nhất và Bội Chung Nhỏ Nhất

UCLN và BCNN (Bội Chung Nhỏ Nhất) là hai khái niệm song song và có mối liên hệ mật thiết với nhau. BCNN của hai số tự nhiên a và b là số tự nhiên nhỏ nhất khác 0 mà cả a và b đều là ước của nó.

Mối quan hệ quan trọng nhất giữa chúng là:

UCLN(a, b) × BCNN(a, b) = a × b

Công thức này cho phép chúng ta dễ dàng tìm BCNN nếu đã biết UCLN (hoặc ngược lại), mà không cần phải tính toán lại từ đầu.

Ví dụ: Ta đã biết UCLN(72, 108) = 36.

Áp dụng công thức: BCNN(72, 108) = (72 × 108) / UCLN(72, 108) = (72 × 108) / 36 = 2 × 108 = 216.

Hiểu rõ mối liên hệ này giúp bạn giải quyết các bài toán liên quan đến cả hai khái niệm một cách nhanh chóng và chính xác.

Kết Luận

Ước chung lớn nhất không chỉ là một khái niệm toán học đơn thuần mà còn là công cụ hữu ích trong nhiều lĩnh vực của cuộc sống. Từ việc rút gọn phân số đến giải quyết các bài toán chia đều, UCLN chứng tỏ giá trị thực tiễn của mình. Nắm vững các phương pháp tìm UCLN sẽ trang bị cho bạn một kỹ năng quan trọng, giúp bạn tiếp cận và giải quyết các vấn đề một cách logic và hiệu quả hơn.

Hy vọng bài viết này đã cung cấp cho bạn cái nhìn toàn diện và sâu sắc về ước chung lớn nhất. Hãy thực hành các ví dụ và áp dụng kiến thức này vào những bài toán thực tế để củng cố sự hiểu biết của mình nhé!

Câu Hỏi Thường Gặp Về Ước Chung Lớn Nhất (FAQ)

1. Ước chung lớn nhất là gì?

Ước chung lớn nhất (UCLN) của hai hay nhiều số tự nhiên là số tự nhiên lớn nhất mà tất cả các số đó đều chia hết cho nó. Đây là một khái niệm cơ bản trong số học.

2. Tại sao cần phải tìm ước chung lớn nhất?

Tìm UCLN giúp rút gọn phân số về dạng tối giản, giải quyết các bài toán chia đều (tìm số lượng phần lớn nhất), và là nền tảng cho nhiều phép toán số học khác như tìm bội chung nhỏ nhất.

3. Như thế nào là số nguyên tố cùng nhau?

Hai số được gọi là nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1. Ví dụ, UCLN(7, 10) = 1, nên 7 và 10 là nguyên tố cùng nhau.

4. Có nên sử dụng thuật toán Euclid để tìm UCLN?

Có, thuật toán Euclid là phương pháp hiệu quả nhất để tìm UCLN của hai số, đặc biệt là với các số lớn. Nó nhanh chóng và không yêu cầu phân tích thừa số nguyên tố, giảm thiểu lỗi tính toán.

5. Ước chung lớn nhất có ứng dụng gì trong thực tế?

Trong thực tế, ước chung lớn nhất được dùng để tối giản phân số, giải các bài toán liên quan đến việc chia nhóm hoặc sắp xếp đối tượng sao cho đồng đều và hiệu quả nhất, và cả trong lập trình máy tính.

6. Làm thế nào để phân biệt ước chung lớn nhất và bội chung nhỏ nhất?

UCLN là số lớn nhất chia hết cho tất cả các số, còn BCNN là số nhỏ nhất mà tất cả các số đều là ước của nó. UCLN liên quan đến việc "chia" (tối đa hóa phần chia), trong khi BCNN liên quan đến việc "gộp" (tìm điểm chung nhỏ nhất).